Ordinary Differential Equations (ODEs)

Ordinary Differential Equations (ODEs)#

General steps to solve ODEs (in the old way)#

  • Define a model function representing the right-hand-side (RHS) of the system.

    • Out-of-place form: f(u, p, t) where u is the state variable(s), p is the parameter(s), and t is the independent variable (usually time). The output is the right hand side (RHS) of the differential equation system.

    • In-place form: f!(du, u, p, t), where the output is saved to du. The rest is the same as the out-of-place form. The in-place function may be faster since it does not allocate a new array in each call.

  • Initial conditions (u0) for the state variable(s).

  • (Optional) parameter(s) p.

  • Define a problem (e.g. ODEProblem) using the model function (f), initial condition(s) (u0), simulation time span (tspan == (tstart, tend)), and parameter(s) p.

  • Solve the problem by calling solve(prob).

Radioactive decay#

The decaying rate of a nuclear isotope is proprotional to its concentration (number):

\[ \frac{d}{dt}C(t) = - \lambda C(t) \]

State variable(s)

  • \(C(t)\): The concentration (number) of a decaying nuclear isotope.

Parameter(s)

  • \(\lambda\): The rate constant of nuclear decay. The half-life: \(t_{\frac{1}{2}} = \frac{ln2}{\lambda}\).

using OrdinaryDiffEq
using Plots

The exponential decay ODE model, out-of-place (3-parameter) form

expdecay(u, p, t) = p * u

expdecay (generic function with 1 method)

p = -1.0 ## Parameter
u0 = 1.0 ## Initial condition
tspan = (0.0, 2.0) ## Simulation start and end time points
prob = ODEProblem(expdecay, u0, tspan, p) ## Define the problem
sol = solve(prob) ## Solve the problem

retcode: Success
Interpolation: 3rd order Hermite
t: 8-element Vector{Float64}:
 0.0
 0.10001999200479662
 0.34208427066999536
 0.6553980136343391
 1.0312652525315806
 1.4709405856363595
 1.9659576669700232
 2.0
u: 8-element Vector{Float64}:
 1.0
 0.9048193287657775
 0.7102883621328676
 0.5192354400036404
 0.35655576576996556
 0.2297097907863828
 0.14002247272452764
 0.1353360028400881

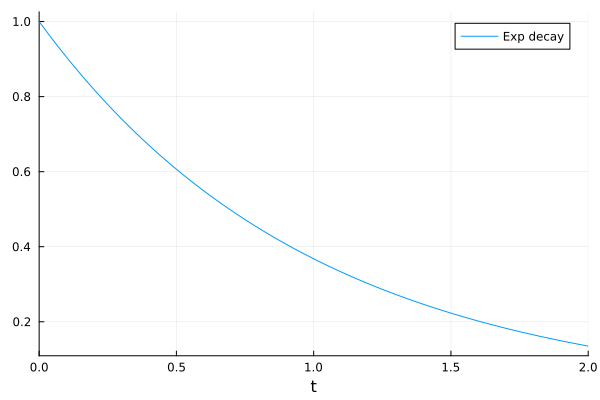
Visualize the solution with Plots.jl.

plot(sol, label="Exp decay")
_images/ca7c012538e49660eb46d7971458b53e17561a928a4dd8cc9379f56b5e0ef578.png

Solution handling: https://docs.sciml.ai/DiffEqDocs/stable/basics/solution/ The mostly used feature is sol(t), the state variables at time t. t could be a scalar or a vector-like sequence. The result state variables are calculated with interpolation.

sol(1.0)

0.3678796381978344

sol(0.0:0.1:2.0)

t: 0.0:0.1:2.0
u: 21-element Vector{Float64}:
 1.0
 0.9048374180989603
 0.8187305973051514
 0.7408182261974484
 0.670319782243577
 0.6065302341562359
 0.5488116548085096
 0.49658509875978446
 0.4493280239179766
 0.4065692349272286
 ⋮
 0.30119273799114377
 0.2725309051375336
 0.24659717503493142
 0.22313045099430742
 0.20189530933816474
 0.18268185222253558
 0.16529821250790575
 0.14956912660454402
 0.13533600284008812

sol.t: time points by the solver.

sol.t

8-element Vector{Float64}:
 0.0
 0.10001999200479662
 0.34208427066999536
 0.6553980136343391
 1.0312652525315806
 1.4709405856363595
 1.9659576669700232
 2.0

sol.u: state variables at sol.t.

sol.u

8-element Vector{Float64}:
 1.0
 0.9048193287657775
 0.7102883621328676
 0.5192354400036404
 0.35655576576996556
 0.2297097907863828
 0.14002247272452764
 0.1353360028400881

The SIR model#

A more complicated example is the SIR model describing infectious disease spreading. There are 3 state variables and 2 parameters.

\[\begin{split} \begin{align} \frac{d}{dt}S(t) &= - \beta S(t)I(t) \\ \frac{d}{dt}I(t) &= \beta S(t)I(t) - \gamma I(t) \\ \frac{d}{dt}R(t) &= \gamma I(t) \end{align} \end{split}\]

State variable(s)

  • \(S(t)\) : the fraction of susceptible people

  • \(I(t)\) : the fraction of infectious people

  • \(R(t)\) : the fraction of recovered (or removed) people

Parameter(s)

  • \(\beta\) : the rate of infection when susceptible and infectious people meet

  • \(\gamma\) : the rate of recovery of infectious people

using OrdinaryDiffEq
using Plots

Here we use the in-place form: f!(du, u, p ,t) for the SIR model. The output is written to the first argument du, without allocating a new array in each function call.

function sir!(du, u, p, t)
    s, i, r = u
    β, γ = p
    v1 = β * s * i
    v2 = γ * i
    du[1] = -v1
    du[2] = v1 - v2
    du[3] = v2
    return nothing
end

sir! (generic function with 1 method)

Setup parameters, initial conditions, time span, and the ODE problem.

p = (β=1.0, γ=0.3)
u0 = [0.99, 0.01, 0.00]
tspan = (0.0, 20.0)
prob = ODEProblem(sir!, u0, tspan, p)

ODEProblem with uType Vector{Float64} and tType Float64. In-place: true
timespan: (0.0, 20.0)
u0: 3-element Vector{Float64}:
 0.99
 0.01
 0.0

Solve the problem

sol = solve(prob)

retcode: Success
Interpolation: 3rd order Hermite
t: 17-element Vector{Float64}:
  0.0
  0.08921318693905476
  0.3702862715172094
  0.7984257132319627
  1.3237271485666187
  1.991841832691831
  2.7923706947355837
  3.754781614278828
  4.901904318934307
  6.260476636498209
  7.7648912410433075
  9.39040980993922
 11.483861023017885
 13.372369854616487
 15.961357172044833
 18.681426667664056
 20.0
u: 17-element Vector{Vector{Float64}}:
 [0.99, 0.01, 0.0]
 [0.9890894703413342, 0.010634484617786016, 0.00027604504087978485]
 [0.9858331594901347, 0.012901496825852227, 0.0012653436840130785]
 [0.9795270529591532, 0.017282420996456258, 0.003190526044390597]
 [0.9689082167415561, 0.02463126703444545, 0.006460516223998508]
 [0.9490552312363142, 0.03827338797605378, 0.012671380787632141]
 [0.9118629475333939, 0.06347250098224964, 0.024664551484356558]
 [0.8398871089274511, 0.11078176031568547, 0.049331130756863524]
 [0.7075842068024722, 0.19166147882272844, 0.1007543143747994]
 [0.508146028721987, 0.29177419341470584, 0.20007977786330722]
 [0.31213222024413995, 0.3415879120018046, 0.34627986775405545]
 [0.18215683096365565, 0.3099983134156389, 0.5078448556207055]
 [0.10427205468919205, 0.22061114011133276, 0.6751168051994751]
 [0.07386737407725845, 0.14760143051851143, 0.7785311954042301]
 [0.05545028910907714, 0.07997076922865315, 0.8645789416622697]
 [0.047334990695892025, 0.04060565321383335, 0.9120593560902746]
 [0.04522885458929332, 0.029057416110814603, 0.925713729299892]

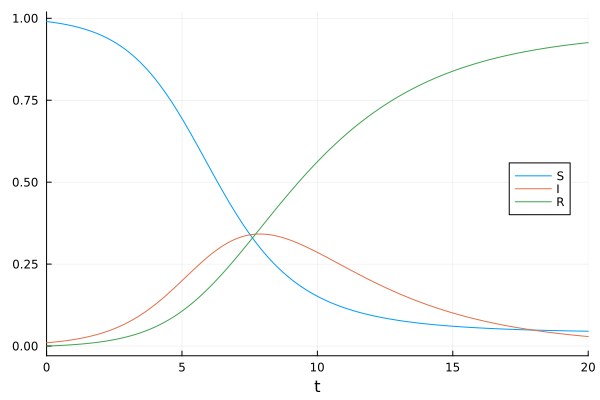
Visualize the solution

plot(sol, labels=["S" "I" "R"], legend=:right)
_images/31b518e413cfef1b0c654701a189e326b562f4f525fbf08f2a6ff4360fe974fd.png

sol[i]: all components at time step i

sol[2]

3-element Vector{Float64}:
 0.9890894703413342
 0.010634484617786016
 0.00027604504087978485

sol[i, j]: ith component at time step j

sol[1, 2]

0.9890894703413342

sol[i, :]: the time series for the ith component.

sol[1, :]

17-element Vector{Float64}:
 0.99
 0.9890894703413342
 0.9858331594901347
 0.9795270529591532
 0.9689082167415561
 0.9490552312363142
 0.9118629475333939
 0.8398871089274511
 0.7075842068024722
 0.508146028721987
 0.31213222024413995
 0.18215683096365565
 0.10427205468919205
 0.07386737407725845
 0.05545028910907714
 0.047334990695892025
 0.04522885458929332

sol(t,idxs=1): the 1st element in time point(s) t with interpolation. t can be a scalar or a vector.

sol(10, idxs=2)

0.28576194586813003

sol(0.0:0.1:20.0, idxs=2)

t: 0.0:0.1:20.0
u: 201-element Vector{Float64}:
 0.01
 0.010713819530291442
 0.01147737632963402
 0.012293955863322855
 0.013167034902663112
 0.014100286700885235
 0.015097588761311391
 0.016163031360643162
 0.01730091874845442
 0.018515771780096318
 ⋮
 0.03561030823283819
 0.03471833422630802
 0.03384816241692694
 0.03299928861769087
 0.032171218254199684
 0.031363466364657075
 0.030575557599870556
 0.029807026223251362
 0.029057416110814645

Lorenz system#

The Lorenz system is a system of ordinary differential equations having chaotic solutions for certain parameter values and initial conditions. (Wikipedia)

\[\begin{split} \begin{align} \frac{dx}{dt} &=& \sigma(y-x) \\ \frac{dy}{dt} &=& x(\rho - z) -y \\ \frac{dz}{dt} &=& xy - \beta z \end{align} \end{split}\]

In this example, we will use NamedTuple for the parameters and ComponentArrays.jl for the state variaBLE to access elements by their names.

using ComponentArrays
using OrdinaryDiffEq
using Plots

function lorenz!(du, u, p, t)
    du.x = p.σ * (u.y - u.x)
    du.y = u.x * (p.ρ - u.z) - u.y
    du.z = u.x * u.y - p.β * u.z
    return nothing
end

lorenz! (generic function with 1 method)

u0 = ComponentArray(x=1.0, y=0.0, z=0.0)
p = (σ=10.0, ρ=28.0, β=8 / 3)
tspan = (0.0, 100.0)
prob = ODEProblem(lorenz!, u0, tspan, p)
sol = solve(prob)

retcode: Success
Interpolation: 3rd order Hermite
t: 1292-element Vector{Float64}:
   0.0
   3.5678604836301404e-5
   0.0003924646531993154
   0.003262408731175873
   0.009058076622686189
   0.01695647090176743
   0.027689960116420883
   0.041856352219618344
   0.060240411865493296
   0.08368541210909924
   ⋮
  99.43545175575305
  99.50217600300971
  99.56297541572351
  99.62622492183432
  99.69561088424294
  99.77387244562912
  99.86354266863755
  99.93826978918452
 100.0
u: 1292-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(x = 1, y = 2, z = 3)}}}}:
 ComponentVector{Float64}(x = 1.0, y = 0.0, z = 0.0)
 ComponentVector{Float64}(x = 0.9996434557625105, y = 0.0009988049817849058, z = 1.781434788799189e-8)
 ComponentVector{Float64}(x = 0.9961045497425811, y = 0.010965399721242457, z = 2.1469553658389193e-6)
 ComponentVector{Float64}(x = 0.9693591548287857, y = 0.0897706331002921, z = 0.00014380191884671585)
 ComponentVector{Float64}(x = 0.9242043547708632, y = 0.24228915014052968, z = 0.0010461625485930237)
 ComponentVector{Float64}(x = 0.8800455783133068, y = 0.43873649717821195, z = 0.003424260078582332)
 ComponentVector{Float64}(x = 0.8483309823046307, y = 0.6915629680633586, z = 0.008487625469885364)
 ComponentVector{Float64}(x = 0.8495036699348377, y = 1.0145426764822272, z = 0.01821209108471829)
 ComponentVector{Float64}(x = 0.9139069585506618, y = 1.442559985646147, z = 0.03669382222358562)
 ComponentVector{Float64}(x = 1.0888638225734468, y = 2.0523265829961646, z = 0.07402573595703686)
 ⋮
 ComponentVector{Float64}(x = 1.2013409155396158, y = -2.429012698730855, z = 25.83593282347909)
 ComponentVector{Float64}(x = -0.4985909866565941, y = -2.2431908075030083, z = 21.591758421186338)
 ComponentVector{Float64}(x = -1.3554328352527145, y = -2.5773570617802326, z = 18.48962628032902)
 ComponentVector{Float64}(x = -2.1618698772305467, y = -3.5957801801676297, z = 15.934724265473792)
 ComponentVector{Float64}(x = -3.433783468673715, y = -5.786446127166032, z = 14.065327938066913)
 ComponentVector{Float64}(x = -5.971873646288483, y = -10.261846004477597, z = 14.060290896024572)
 ComponentVector{Float64}(x = -10.941900618598972, y = -17.312154206417734, z = 20.65905960858999)
 ComponentVector{Float64}(x = -14.71738043327772, y = -16.96871551014668, z = 33.06627229408802)
 ComponentVector{Float64}(x = -13.714517151605754, y = -8.323306384833089, z = 38.798231477265624)

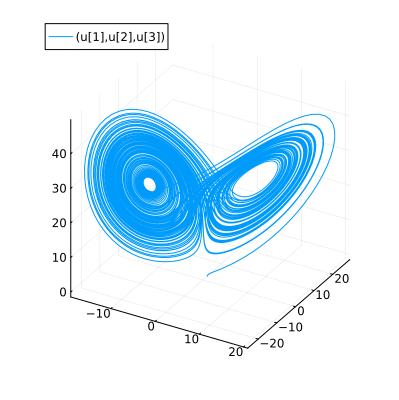
idxs=(1, 2, 3) makes a phase plot with 1st, 2nd, and the 3rd state variable.

plot(sol, idxs=(1, 2, 3), size=(400, 400))
_images/69ae7419d48d5d0bd163f0af2c426cc64508e2b9ac64b8cafdea8c30317b0fe8.png

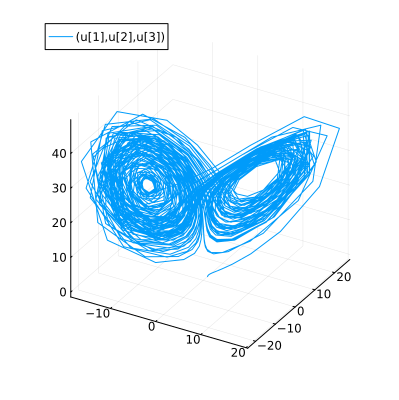
The plot recipe is using interpolation for smoothing. You can turn off denseplot to see the difference.

plot(sol, idxs=(1, 2, 3), denseplot=false, size=(400, 400))
_images/20ae56a47378ddb7075aaafd1faca8a8dabc33b3da2322d853e9b677b658e541.png

The zeroth variable in idxs is the independent variable (usually time). The following command plots the time series of the second state variable (y).

plot(sol, idxs=(0, 2))
_images/dbd2bfa29996ed39b2b679b2dd70395dc9abde6ad7a1b1b54d61526feba0f7e0.png

Non-autonomous ODEs#

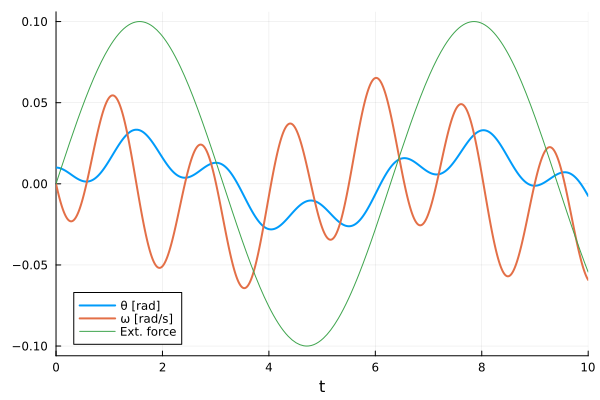
In non-autonomous ODEs, term(s) in the right-hand-side (RHS) maybe time-dependent. For example, in this pendulum model has an external, time-dependent, force.

\[\begin{split} \begin{aligned} \dot{\theta} &= \omega(t) \\ \dot{\omega} &= -1.5\frac{g}{l}sin(\theta(t)) + \frac{3}{ml^2}M(t) \end{aligned} \end{split}\]

  • \(\theta\): pendulum angle

  • \(\omega\): angular rate

  • M: time-dependent external torque

  • \(l\): pendulum length

  • \(g\): gradational acceleration

using OrdinaryDiffEq
using Plots

function pendulum!(du, u, p, t)
    l = 1.0                             ## length [m]
    m = 1.0                             ## mass [kg]
    g = 9.81                            ## gravitational acceleration [m/s²]
    du[1] = u[2]                        ## θ'(t) = ω(t)
    du[2] = -3g / (2l) * sin(u[1]) + 3 / (m * l^2) * p(t) # ω'(t) = -3g/(2l) sin θ(t) + 3/(ml^2)M(t)
end

u0 = [0.01, 0.0]                     ## initial angular deflection [rad] and angular velocity [rad/s]
tspan = (0.0, 10.0)                  ## time interval

M = t -> 0.1 * sin(t)                   ## external torque [Nm] as the parameter for the pendulum model

prob = ODEProblem(pendulum!, u0, tspan, M)
sol = solve(prob)

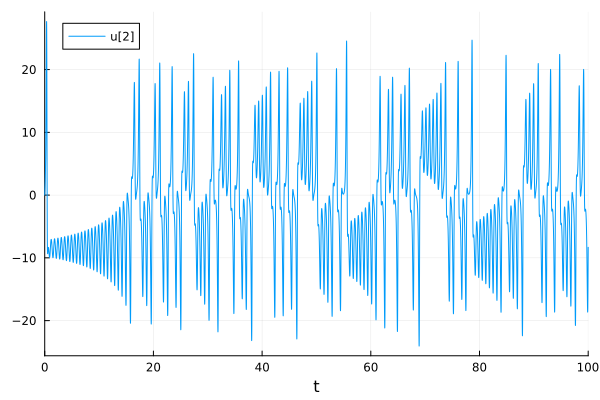
plot(sol, linewidth=2, xaxis="t", label=["θ [rad]" "ω [rad/s]"])
plot!(M, tspan..., label="Ext. force")
_images/b70a9fe5fddc4946f6519a2f823149a21b4dba89b50e2e5d5ba7be9e0c9b88bb.png

Linear ODE system#

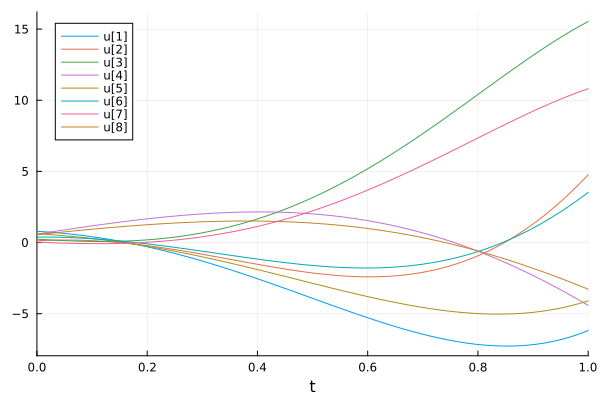
The ODE system could be anything as long as it returns the derivatives of state variables. In this example, the ODE system is described by a matrix differential operator.

\(\dot{u} = Au\)

using OrdinaryDiffEq
using Plots

A = [
    1.0 0 0 -5
    4 -2 4 -3
    -4 0 0 1
    5 -2 2 3
]

u0 = rand(4, 2)

tspan = (0.0, 1.0)
f = (u, p, t) -> A * u
prob = ODEProblem(f, u0, tspan)
sol = solve(prob)
plot(sol)
_images/4385b44e4efd8ba5c360886321b8f248ac5ddc59c9f90a768a041f6f8076b4ed.png

This notebook was generated using Literate.jl.