ModelingToolkit: define ODEs with symbolic expressions

ModelingToolkit: define ODEs with symbolic expressions#

You can also define ODE systems symbolically using ModelingToolkit.jl (MTK) and let MTK generate high-performace ODE functions.

  • transforming and simplifying expressions for performance

  • Jacobian and Hessian generation

  • accessing eliminated states (called observed variables)

  • building and connecting subsystems programatically (component-based modeling)

See also Simulating Big Models in Julia with ModelingToolkit @ JuliaCon 2021 Workshop.

Radioactive decay#

Here we use the same example of decaying radioactive elements

using ModelingToolkit
using OrdinaryDiffEq
using Plots

independent variable (time) and dependent variables

@independent_variables t
@variables c(t) RHS(t)
\[\begin{split} \begin{equation} \left[ \begin{array}{c} c\left( t \right) \\ \mathtt{RHS}\left( t \right) \\ \end{array} \right] \end{equation} \end{split}\]

parameters: decay rate

@parameters λ
\[\begin{split} \begin{equation} \left[ \begin{array}{c} \lambda \\ \end{array} \right] \end{equation} \end{split}\]

Differential operator w.r.t. time

D = Differential(t)

Differential(t)

Equations in MTK use the tilde character (~) for equality. Every MTK system requires a name. The @named macro simply ensures that the symbolic name matches the name in the REPL.

eqs = [
    RHS ~ -λ * c
    D(c) ~ RHS
]

@named sys = ODESystem(eqs, t)
\[\begin{split} \begin{align} \frac{\mathrm{d} c\left( t \right)}{\mathrm{d}t} &= \mathtt{RHS}\left( t \right) \\ \mathtt{RHS}\left( t \right) &= - c\left( t \right) \lambda \end{align} \end{split}\]

structural_simplify() simplifies the two equations to one. You can also use @mtkbuild sys = ODESystem(eqs, t), which automatically simplifies the system.

sys = structural_simplify(sys)
\[ \begin{align} \frac{\mathrm{d} c\left( t \right)}{\mathrm{d}t} &= \mathtt{RHS}\left( t \right) \end{align} \]

Setup initial conditions, time span, parameter values, the ODEProblem, and solve the problem.

p = [λ => 1.0]
u0 = [c => 1.0]
tspan = (0.0, 2.0)
prob = ODEProblem(sys, u0, tspan, p)
sol = solve(prob)

retcode: Success
Interpolation: 3rd order Hermite
t: 8-element Vector{Float64}:
 0.0
 0.10001999200479662
 0.34208427066999536
 0.6553980136343391
 1.0312652525315806
 1.4709405856363595
 1.9659576669700232
 2.0
u: 8-element Vector{Vector{Float64}}:
 [1.0]
 [0.9048193287657775]
 [0.7102883621328676]
 [0.5192354400036404]
 [0.35655576576996556]
 [0.2297097907863828]
 [0.14002247272452764]
 [0.1353360028400881]

Visualize the solution

plot(sol, label="Exp decay")
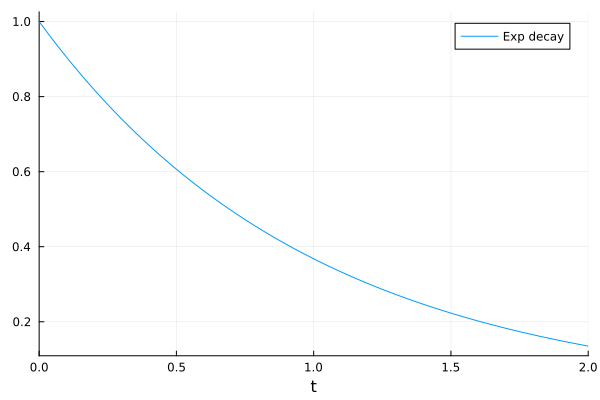
_images/ca7c012538e49660eb46d7971458b53e17561a928a4dd8cc9379f56b5e0ef578.png

The solution interface provides symbolic access. You can access the results of the unknown c directly.

sol[c]

8-element Vector{Float64}:
 1.0
 0.9048193287657775
 0.7102883621328676
 0.5192354400036404
 0.35655576576996556
 0.2297097907863828
 0.14002247272452764
 0.1353360028400881

With interpolations with specified timepoints

sol(0.0:0.1:2.0, idxs=c)

t: 0.0:0.1:2.0
u: 21-element Vector{Float64}:
 1.0
 0.9048374180989603
 0.8187305973051514
 0.7408182261974484
 0.670319782243577
 0.6065302341562359
 0.5488116548085096
 0.49658509875978446
 0.4493280239179766
 0.4065692349272286
 ⋮
 0.30119273799114377
 0.2725309051375336
 0.24659717503493142
 0.22313045099430742
 0.20189530933816474
 0.18268185222253558
 0.16529821250790575
 0.14956912660454402
 0.13533600284008812

The eliminated term (RHS in this example) is still traceable.

plot(sol, idxs=[c, RHS], legend=:right)
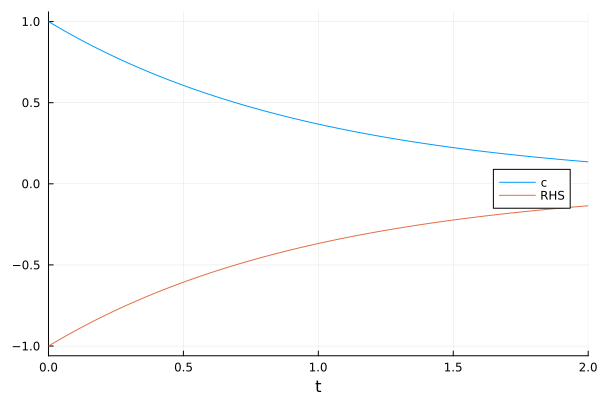
_images/018d3d12fc2503c9110f6270410e0a22c616fac9e3a887d0deddbc3cea0278ff.png

The indexing interface allows symbolic calculations.

plot(sol, idxs=[c * 1000])
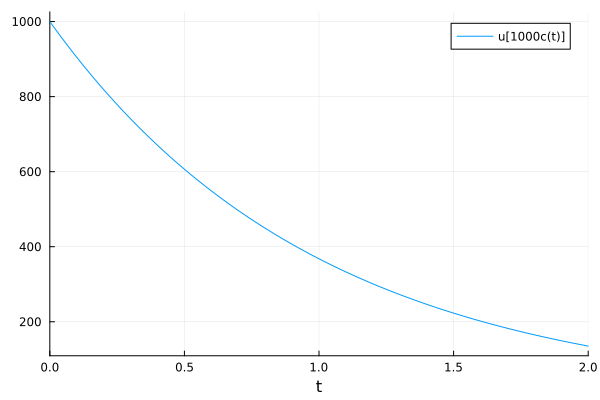
_images/c5c85ca653ea17566dc1763a5eac504b7dad431157a7868d5e7d45fed6de9cb8.png

Lorenz system#

We use the same Lorenz system example as above. Here we setup the initial conditions and parameters with default values.

@independent_variables t
@variables x(t) = 1.0 y(t) = 0.0 z(t) = 0.0
@parameters (σ=10.0, ρ=28.0, β=8 / 3)

D = Differential(t)

eqs = [
    D(x) ~ σ * (y - x)
    D(y) ~ x * (ρ - z) - y
    D(z) ~ x * y - β * z
]

@mtkbuild sys = ODESystem(eqs, t)
\[\begin{split} \begin{align} \frac{\mathrm{d} x\left( t \right)}{\mathrm{d}t} &= \left( - x\left( t \right) + y\left( t \right) \right) \sigma \\ \frac{\mathrm{d} y\left( t \right)}{\mathrm{d}t} &= - y\left( t \right) + x\left( t \right) \left( - z\left( t \right) + \rho \right) \\ \frac{\mathrm{d} z\left( t \right)}{\mathrm{d}t} &= x\left( t \right) y\left( t \right) - z\left( t \right) \beta \end{align} \end{split}\]

Here we are using default values, so we pass empty arrays for initial conditions and parameter values.

tspan = (0.0, 100.0)
prob = ODEProblem(sys, [], tspan, [])
sol = solve(prob)

retcode: Success
Interpolation: 3rd order Hermite
t: 1292-element Vector{Float64}:
   0.0
   3.5678604836301404e-5
   0.0003924646531993154
   0.003262408731175873
   0.009058076622686189
   0.01695647090176743
   0.027689960116420883
   0.041856352219618344
   0.060240411865493296
   0.08368541210909924
   ⋮
  99.43545175575305
  99.50217600300971
  99.56297541572351
  99.62622492183432
  99.69561088424294
  99.77387244562912
  99.86354266863755
  99.93826978918452
 100.0
u: 1292-element Vector{Vector{Float64}}:
 [1.0, 0.0, 0.0]
 [0.9996434557625105, 0.0009988049817849058, 1.781434788799189e-8]
 [0.9961045497425811, 0.010965399721242457, 2.1469553658389193e-6]
 [0.9693591548287857, 0.0897706331002921, 0.00014380191884671585]
 [0.9242043547708632, 0.24228915014052968, 0.0010461625485930237]
 [0.8800455783133068, 0.43873649717821195, 0.003424260078582332]
 [0.8483309823046307, 0.6915629680633586, 0.008487625469885364]
 [0.8495036699348377, 1.0145426764822272, 0.01821209108471829]
 [0.9139069585506618, 1.442559985646147, 0.03669382222358562]
 [1.0888638225734468, 2.0523265829961646, 0.07402573595703686]
 ⋮
 [1.2013409155396158, -2.429012698730855, 25.83593282347909]
 [-0.4985909866565941, -2.2431908075030083, 21.591758421186338]
 [-1.3554328352527145, -2.5773570617802326, 18.48962628032902]
 [-2.1618698772305467, -3.5957801801676297, 15.934724265473792]
 [-3.433783468673715, -5.786446127166032, 14.065327938066913]
 [-5.971873646288483, -10.261846004477597, 14.060290896024572]
 [-10.941900618598972, -17.312154206417734, 20.65905960858999]
 [-14.71738043327772, -16.96871551014668, 33.06627229408802]
 [-13.714517151605754, -8.323306384833089, 38.798231477265624]

Plot the solution with symbols instead of index numbers.

plot(sol, idxs=(x, y, z), size=(400, 400))
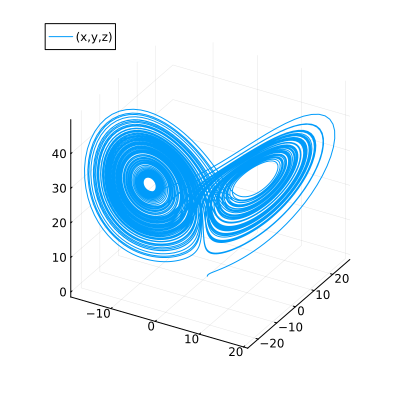
_images/173c8568c4ecb78bd0dd10a91cdf64c5adfaded8277ea318d60d9f228ec4f630.png

Non-autonomous ODEs#

Sometimes a model might have a time-variant external force, which is too complex or impossible to express it symbolically. In such situation, one could apply @register_symbolic to it to exclude it from symbolic transformations and use it numerically.

@independent_variables t
@variables x(t) f(t)
@parameters τ
D = Differential(t)

Differential(t)

Define a time-dependent random external force

value_vector = randn(10)
f_fun(t) = t >= 10 ? value_vector[end] : value_vector[Int(floor(t))+1]

f_fun (generic function with 1 method)

“Register” arbitrary Julia functions to be excluded from symbolic transformations. Just use it as-is.

@register_symbolic f_fun(t)
@mtkbuild fol_external_f = ODESystem([f ~ f_fun(t), D(x) ~ (f - x) / τ], t)

prob = ODEProblem(fol_external_f, [x => 0.0], (0.0, 10.0), [τ => 0.75])
sol = solve(prob)
plot(sol, idxs=[x, f])
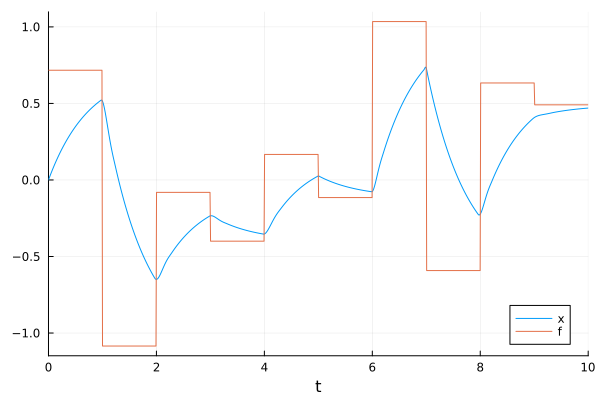
_images/0fc162eac7960892429c4b265b40f090fc5fa94a112b3230dc58c9233b2be749.png

Second-order ODE systems#

ode_order_lowering(sys) automatically transforms a second-order ODE into two first-order ODEs.

using Plots
using ModelingToolkit
using OrdinaryDiffEq

@parameters σ ρ β
@independent_variables t
@variables x(t) y(t) z(t)
D = Differential(t)

eqs = [
    D(D(x)) ~ σ * (y - x),
    D(y) ~ x * (ρ - z) - y,
    D(z) ~ x * y - β * z
]

@mtkbuild sys = ODESystem(eqs, t)
\[\begin{split} \begin{align} \frac{\mathrm{d} \mathtt{xˍt}\left( t \right)}{\mathrm{d}t} &= \left( - x\left( t \right) + y\left( t \right) \right) \sigma \\ \frac{\mathrm{d} y\left( t \right)}{\mathrm{d}t} &= - y\left( t \right) + x\left( t \right) \left( - z\left( t \right) + \rho \right) \\ \frac{\mathrm{d} z\left( t \right)}{\mathrm{d}t} &= x\left( t \right) y\left( t \right) - z\left( t \right) \beta \\ \frac{\mathrm{d} x\left( t \right)}{\mathrm{d}t} &= \mathtt{xˍt}\left( t \right) \end{align} \end{split}\]

Note that you need to provide the initial condition for x’s derivative (D(x)).

u0 = [
    D(x) => 2.0,
    x => 1.0,
    y => 0.0,
    z => 0.0
]

p = [
    σ => 28.0,
    ρ => 10.0,
    β => 8 / 3
]

tspan = (0.0, 100.0)
prob = ODEProblem(sys, u0, tspan, p, jac=true)
sol = solve(prob)
plot(sol, idxs=(x, y, z), label="Trajectory", size=(500, 500))
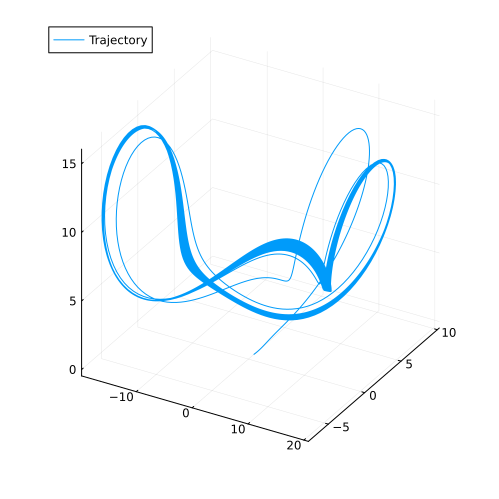
_images/e79f762d742c3eb104eb621a407bde3de2024cd7aa8d789614d59d4d7545590a.png

Composing systems#

By connecting equation(s) to couple ODE systems together, we can build component-based, hierarchical models.

using Plots
using ModelingToolkit
using OrdinaryDiffEq

@parameters σ ρ β
@independent_variables t
@variables x(t) y(t) z(t)
D = Differential(t)

eqs = [
    D(x) ~ σ * (y - x),
    D(y) ~ x * (ρ - z) - y,
    D(z) ~ x * y - β * z
]

@named lorenz1 = ODESystem(eqs, t)
@named lorenz2 = ODESystem(eqs, t)
\[\begin{split} \begin{align} \frac{\mathrm{d} x\left( t \right)}{\mathrm{d}t} &= \left( - x\left( t \right) + y\left( t \right) \right) \sigma \\ \frac{\mathrm{d} y\left( t \right)}{\mathrm{d}t} &= - y\left( t \right) + x\left( t \right) \left( - z\left( t \right) + \rho \right) \\ \frac{\mathrm{d} z\left( t \right)}{\mathrm{d}t} &= x\left( t \right) y\left( t \right) - z\left( t \right) \beta \end{align} \end{split}\]

Define relations (connectors) between the two systems.

@variables a(t)
@parameters γ
connections = [0 ~ lorenz1.x + lorenz2.y + a * γ]
@named connLorenz = ODESystem(connections, t, [a], [γ], systems=[lorenz1, lorenz2])
\[\begin{split} \begin{align} 0 &= \mathtt{lorenz2.y}\left( t \right) + \mathtt{lorenz1.x}\left( t \right) + a\left( t \right) \gamma \\ \frac{\mathrm{d} \mathtt{lorenz1.x}\left( t \right)}{\mathrm{d}t} &= \mathtt{lorenz1.\sigma} \left( - \mathtt{lorenz1.x}\left( t \right) + \mathtt{lorenz1.y}\left( t \right) \right) \\ \frac{\mathrm{d} \mathtt{lorenz1.y}\left( t \right)}{\mathrm{d}t} &= - \mathtt{lorenz1.y}\left( t \right) + \left( \mathtt{lorenz1.\rho} - \mathtt{lorenz1.z}\left( t \right) \right) \mathtt{lorenz1.x}\left( t \right) \\ \frac{\mathrm{d} \mathtt{lorenz1.z}\left( t \right)}{\mathrm{d}t} &= - \mathtt{lorenz1.\beta} \mathtt{lorenz1.z}\left( t \right) + \mathtt{lorenz1.x}\left( t \right) \mathtt{lorenz1.y}\left( t \right) \\ \frac{\mathrm{d} \mathtt{lorenz2.x}\left( t \right)}{\mathrm{d}t} &= \mathtt{lorenz2.\sigma} \left( \mathtt{lorenz2.y}\left( t \right) - \mathtt{lorenz2.x}\left( t \right) \right) \\ \frac{\mathrm{d} \mathtt{lorenz2.y}\left( t \right)}{\mathrm{d}t} &= - \mathtt{lorenz2.y}\left( t \right) + \left( \mathtt{lorenz2.\rho} - \mathtt{lorenz2.z}\left( t \right) \right) \mathtt{lorenz2.x}\left( t \right) \\ \frac{\mathrm{d} \mathtt{lorenz2.z}\left( t \right)}{\mathrm{d}t} &= - \mathtt{lorenz2.\beta} \mathtt{lorenz2.z}\left( t \right) + \mathtt{lorenz2.y}\left( t \right) \mathtt{lorenz2.x}\left( t \right) \end{align} \end{split}\]

All unknown state variables in the combined system

unknowns(connLorenz)

7-element Vector{SymbolicUtils.BasicSymbolic{Real}}:
 a(t)
 lorenz1₊x(t)
 lorenz1₊y(t)
 lorenz1₊z(t)
 lorenz2₊x(t)
 lorenz2₊y(t)
 lorenz2₊z(t)

u0 = [
    lorenz1.x => 1.0, lorenz1.y => 0.0, lorenz1.z => 0.0,
    lorenz2.x => 0.0, lorenz2.y => 1.0, lorenz2.z => 0.0,
    a => 2.0
]

p = [
    lorenz1.σ => 10.0, lorenz1.ρ => 28.0, lorenz1.β => 8 / 3,
    lorenz2.σ => 10.0, lorenz2.ρ => 28.0, lorenz2.β => 8 / 3,
    γ => 2.0
]

tspan = (0.0, 100.0)
sys = connLorenz |> structural_simplify
sol = solve(ODEProblem(sys, u0, tspan, p, jac=true))
plot(sol, idxs=(a, lorenz1.x, lorenz2.x), size=(600, 600))

┌ Warning: Initialization system is overdetermined. 1 equations for 0 unknowns. Initialization will default to using least squares. To suppress this warning pass warn_initialize_determined = false. To make this warning into an error, pass fully_determined = true
└ @ ModelingToolkit ~/.julia/packages/ModelingToolkit/zfOUk/src/systems/diffeqs/abstractodesystem.jl:1291
_images/8b7d310ca60530ccb7d2f07bba94d88440b19616d6031e0c0ffa8245d28d2f2e.png

Convert existing functions into MTK systems#

modelingtoolkitize(prob) generates MKT systems from regular DE problems. I t can also generate analytic Jacobin functions for faster solving.

Example: DAE index reduction for the pendulum problem, which cannot be solved by regular ODE solvers.

using Plots
using ModelingToolkit
using OrdinaryDiffEq
using LinearAlgebra

function pendulum!(du, u, p, t)
    x, dx, y, dy, T = u
    g, L = p
    du[1] = dx
    du[2] = T * x
    du[3] = dy
    du[4] = T * y - g
    # Do not write your function like this after you've learned MTK
    du[5] = x^2 + y^2 - L^2
    return nothing
end

pendulum_fun! = ODEFunction(pendulum!, mass_matrix=Diagonal([1, 1, 1, 1, 0]))
u0 = [1.0, 0.0, 0.0, 0.0, 0.0]
p = [9.8, 1.0]
tspan = (0.0, 10.0)
pendulum_prob = ODEProblem(pendulum_fun!, u0, tspan, p)

ODEProblem with uType Vector{Float64} and tType Float64. In-place: true
timespan: (0.0, 10.0)
u0: 5-element Vector{Float64}:
 1.0
 0.0
 0.0
 0.0
 0.0

Convert the ODE problem into a MTK system.

tracedSys = modelingtoolkitize(pendulum_prob)
\[\begin{split} \begin{align} \frac{\mathrm{d} \mathtt{x_1}\left( t \right)}{\mathrm{d}t} &= \mathtt{x_2}\left( t \right) \\ \frac{\mathrm{d} \mathtt{x_2}\left( t \right)}{\mathrm{d}t} &= \mathtt{x_1}\left( t \right) \mathtt{x_5}\left( t \right) \\ \frac{\mathrm{d} \mathtt{x_3}\left( t \right)}{\mathrm{d}t} &= \mathtt{x_4}\left( t \right) \\ \frac{\mathrm{d} \mathtt{x_4}\left( t \right)}{\mathrm{d}t} &= - \mathtt{\alpha_1} + \mathtt{x_3}\left( t \right) \mathtt{x_5}\left( t \right) \\ 0 &= \left( \mathtt{x_1}\left( t \right) \right)^{2} + \left( \mathtt{x_3}\left( t \right) \right)^{2} - \mathtt{\alpha_2}^{2} \end{align} \end{split}\]

structural_simplify() and dae_index_lowering() transform the index-3 DAE into an index-0 ODE.

pendulumSys = tracedSys |> dae_index_lowering |> structural_simplify
\[\begin{split} \begin{align} \frac{\mathrm{d} \mathtt{x_1}\left( t \right)}{\mathrm{d}t} &= \mathtt{x_2}\left( t \right) \\ \frac{\mathrm{d} \mathtt{x_2}\left( t \right)}{\mathrm{d}t} &= \mathtt{x_1}\left( t \right) \mathtt{x_5}\left( t \right) \\ \frac{\mathrm{d} \mathtt{x_3}\left( t \right)}{\mathrm{d}t} &= \mathtt{x_4}\left( t \right) \\ \frac{\mathrm{d} \mathtt{x_4}\left( t \right)}{\mathrm{d}t} &= - \mathtt{\alpha_1} + \mathtt{x_3}\left( t \right) \mathtt{x_5}\left( t \right) \\ 0 &= 2 \left( \mathtt{x_4}\left( t \right) \right)^{2} + 2 \left( \mathtt{x_2}\left( t \right) \right)^{2} + 2 \left( \mathtt{x_1}\left( t \right) \right)^{2} \mathtt{x_5}\left( t \right) + 2 \mathtt{x_3}\left( t \right) \left( - \mathtt{\alpha_1} + \mathtt{x_3}\left( t \right) \mathtt{x_5}\left( t \right) \right) \end{align} \end{split}\]

The default u0 is included in the system already so one can use an empty array [] as the initial conditions.

prob = ODEProblem(pendulumSys, [], tspan)
sol = solve(prob, Rodas5P(), abstol=1e-8, reltol=1e-8)

retcode: Success
Interpolation: specialized 4rd order "free" stiffness-aware interpolation
t: 1305-element Vector{Float64}:
  0.0
  1.0e-6
  1.1e-5
  0.00011099999999999999
  0.0010466037811921202
  0.004063045474513508
  0.00794188545926928
  0.0121077885763386
  0.016784515118072017
  0.02172605785948642
  ⋮
  9.939437955690178
  9.947439461345477
  9.955440967000776
  9.963442472656075
  9.971443978311374
  9.979445483966673
  9.987446989621972
  9.995448495277271
 10.0
u: 1305-element Vector{Vector{Float64}}:
 [1.0, 0.0, 0.0, 0.0, 0.0]
 [1.0, -4.8019999999999657e-17, -4.900000000000009e-12, -9.800000000000072e-6, -1.4405999999999968e-10]
 [1.0, -6.391462000000028e-14, -5.929000000000031e-10, -0.00010780000000000034, -1.7431260000000092e-8]
 [0.9999999999999981, -6.567364061999976e-11, -6.037289999999992e-8, -0.0010878000000000023, -1.7749632599999965e-6]
 [0.9999999999855956, -5.5051486974382846e-8, -5.367359426515357e-6, -0.010256717055505578, -0.0001578003671397977]
 [0.9999999967283344, -3.2208997265909783e-6, -8.089085867954903e-5, -0.039817845493907975, -0.0023781912454561662]
 [0.9999999522408447, -2.405431542914682e-5, -0.0003090603628628303, -0.07783047304029803, -0.009086374669453116]
 [0.9999997419989658, -8.523472721281003e-5, -0.0007183327924732369, -0.11865629131197372, -0.02111898410081311]
 [0.9999990472098922, -0.00022706401192704043, -0.0013804272178232551, -0.16448806008980102, -0.0405845602082515]
 [0.9999973252355406, -0.0004924523961325739, -0.002312903316891978, -0.21291468362508234, -0.06799935752282055]
 ⋮
 [0.5278328468315517, -3.46542704204018, -0.8493482890935694, -2.153611478391067, -24.97083945477396]
 [0.49968697637336584, -3.5691094793655016, -0.8662060702076898, -2.058906753238232, -25.46645820431887]
 [0.4707267025772791, -3.6689096678612887, -0.8822790952663302, -1.9574914139213448, -25.939005126803664]
 [0.44098499714511497, -3.764352110346217, -0.8975144916923492, -1.8495777213227487, -26.386925768514566]
 [0.4104985982284546, -3.854971511620498, -0.9118612456942748, -1.7354179849967872, -26.808720324031054]
 [0.3793079133173193, -3.9403166522077813, -0.9252705212441931, -1.6153041265381833, -27.202953014175414]
 [0.3474568910912323, -4.019954264375764, -0.9376959738977672, -1.4895668254758865, -27.56826131232076]
 [0.3149928624136064, -4.093472860333704, -0.9490940560881269, -1.358574241809813, -27.903364920031095]
 [0.29627197045136683, -4.132413586252476, -0.9551036332437005, -1.2818696081505243, -28.08004648349895]

plot(sol, idxs=unknowns(tracedSys))
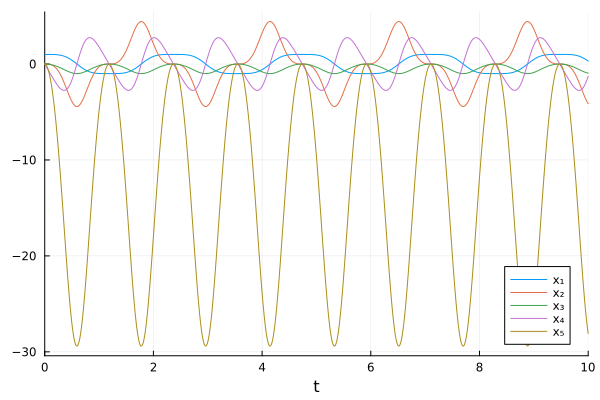
_images/a73f050fc121202750885436e1c4d8ce4c11a8d42326c107164dac53f03d54e6.png

This notebook was generated using Literate.jl.