Calalyst tips

Conservation laws

We can use conservation laws to eliminate some unknown variables. For example, in the chemical reaction A + B <--> C, given the initial concentrations of A, B, and C, the solver needs to find only one of [A], [B], and [C] instead of all three.

using Catalyst
using ModelingToolkit
using DifferentialEquations
using Plots

rn = @reaction_network begin
    (k₊, k₋), A + B <--> C
end

\[ \begin{align*} \mathrm{A} + \mathrm{B} &\xrightleftharpoons[\mathtt{k_-}]{\mathtt{k.}} \mathrm{C} \end{align*} \]

Set initial condition and parameter values

setdefaults!(rn, [:A => 1.0, :B => 2.0, :C => 0.0, :k₊ => 1.0, :k₋ => 1.0])

Let’s convert it to a system of ODEs, using the conservation laws to eliminate two species, leaving only one of them as the state variable. The conserved quantities will be denoted as Γs

osys = convert(ODESystem, rn; remove_conserved=true) |> structural_simplify

┌ Warning: You are creating a system or problem while eliminating conserved quantities. Please note,
│         due to limitations / design choices in ModelingToolkit if you use the created system to
│         create a problem (e.g. an `ODEProblem`), or are directly creating a problem, you *should not*
│         modify that problem's initial conditions for species (e.g. using `remake`). Changing initial
│         conditions must be done by creating a new Problem from your reaction system or the
│         ModelingToolkit system you converted it into with the new initial condition map.
│         Modification of parameter values is still possible, *except* for the modification of any
│         conservation law constants (Γ), which is not possible. You might
│         get this warning when creating a problem directly.
│ 
│         You can remove this warning by setting `remove_conserved_warn = false`.
└ @ Catalyst ~/.julia/packages/Catalyst/48wH3/src/reactionsystem_conversions.jl:456

\[ \begin{align} \frac{\mathrm{d} A\left( t \right)}{\mathrm{d}t} &= \mathtt{k{_-}} \left( - A\left( t \right) + \Gamma_{2} \right) + \mathtt{k.} \left( - A\left( t \right) - \Gamma_{1} \right) A\left( t \right) \end{align} \]

Only one (unknown) state variable need to be solved

unknowns(osys)

1-element Vector{SymbolicUtils.BasicSymbolic{Real}}:
 A(t)

The other two are constrained by conserved quantities

observed(osys)

\[\begin{split} \begin{align} B\left( t \right) &= A\left( t \right) + \Gamma_{1} \\ C\left( t \right) &= - A\left( t \right) + \Gamma_{2} \end{align} \end{split}\]

Solve the problem

oprob = ODEProblem(osys, [], (0.0, 10.0), [])
sol = solve(oprob, Tsit5())

┌ Warning: Initialization system is overdetermined. 2 equations for 0 unknowns. Initialization will default to using least squares. To suppress this warning pass warn_initialize_determined = false. To make this warning into an error, pass fully_determined = true
└ @ ModelingToolkit ~/.julia/packages/ModelingToolkit/zfOUk/src/systems/diffeqs/abstractodesystem.jl:1291

retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 19-element Vector{Float64}:
  0.0
  0.06602162921791198
  0.16167383723177658
  0.27797398569864795
  0.42472768210212675
  0.5991542465684496
  0.8069250399875878
  1.0494129741596487
  1.3328285260259545
  1.6634553095820483
  2.0523543727756204
  2.514619744984259
  3.073985028187367
  3.7668739415643824
  4.65256513049854
  5.821585305489345
  7.328825483832256
  8.975283435170365
 10.0
u: 19-element Vector{Vector{Float64}}:
 [1.0]
 [0.8836569748526829]
 [0.7588242777314499]
 [0.6540331462534721]
 [0.5681302593629073]
 [0.5062418977317176]
 [0.46461886630918997]
 [0.43937914557022106]
 [0.42544919657534686]
 [0.4186148714289667]
 [0.4156790083953944]
 [0.4146117644861058]
 [0.4142972990536097]
 [0.4142270387749867]
 [0.4142160588486048]
 [0.4142152933849376]
 [0.4142196830866055]
 [0.41425212965225616]
 [0.4142262306892306]

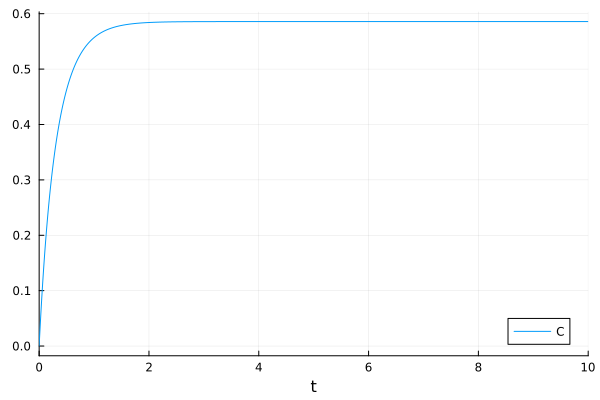
You can still trace the eliminated variable

plot(sol, idxs=osys.C)

---

This notebook was generated using Literate.jl.