Use smooth functions

Use smooth functions#

Use smooth and differentiable functions instead of discontinuities for automatic differentiation (AD) and differential equation solvers.

Heaviside step function#

A Heaviside step function (0 when x < a, 1 when x > a) could be approximated with a steep logistic function.

using Plots

The function output switches from zero to one around x=0. k is the steepness of the function.

function smoothheaviside(x, k=1000)
    return 1 / (1 + exp(-k * x))
end

plot(smoothheaviside, -1, 1)

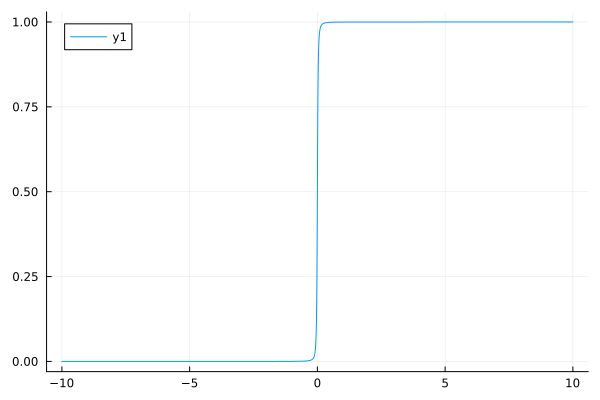
### Smooth step function with `sqrt`
function smoothstep_sqrt(x; c=(1//2)^10)
    0.5 * (x / (sqrt(x^2 + c)) + 1)
end

plot(smoothstep_sqrt, -10, 10)
../_images/83626c6ebf9c51a61bbae6a6fe149c76063f895cf20f09c534ed1a76f5713c6f.png

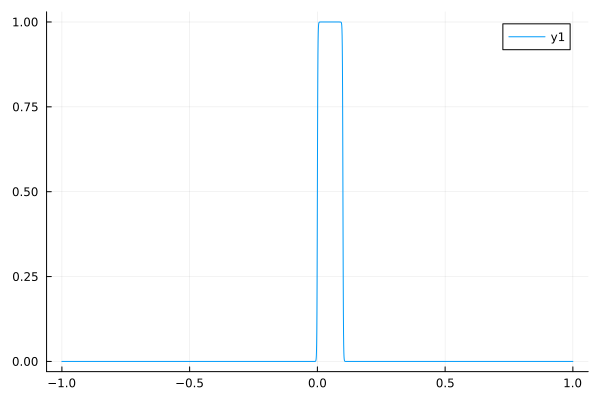
Smooth single pulse#

A single pulse could be built with a product of two step functions.

function singlepulse(x, t0=0, t1=0.1, k=1000)
    smoothheaviside(x - t0, k) * smoothheaviside(t1 - x, k)
end

plot(singlepulse, -1, 1)
../_images/409d0efb1d39019a1a48f90bf895651f0ed57125a9cdfb70dfa2ce152c710f85.png

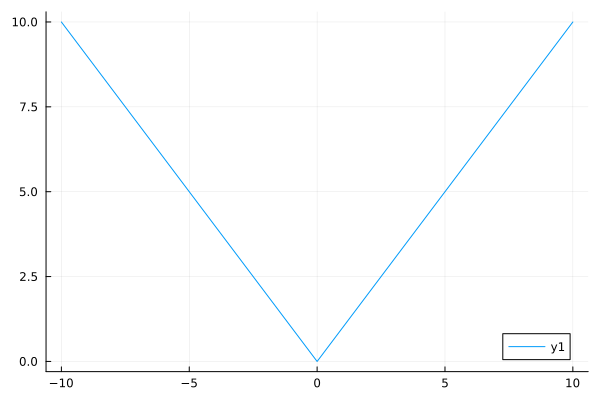
Smooth absolute value#

Inspired by: https://discourse.julialang.org/t/smooth-approximation-to-max-0-x/109383/13

Approximate abs(x)

function smoothabs(x; c=(1//2)^10)
    hypot(x, c) - c
end

plot(smoothabs, -10, 10)

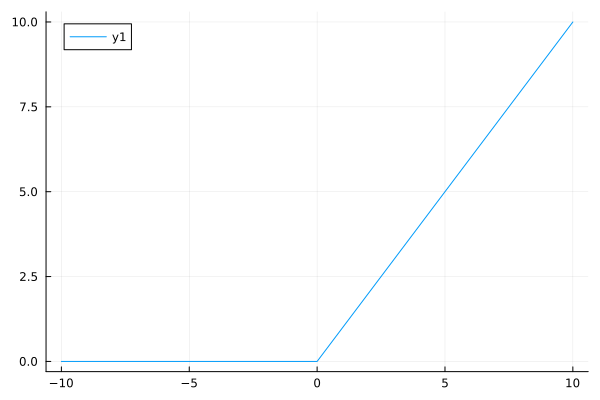
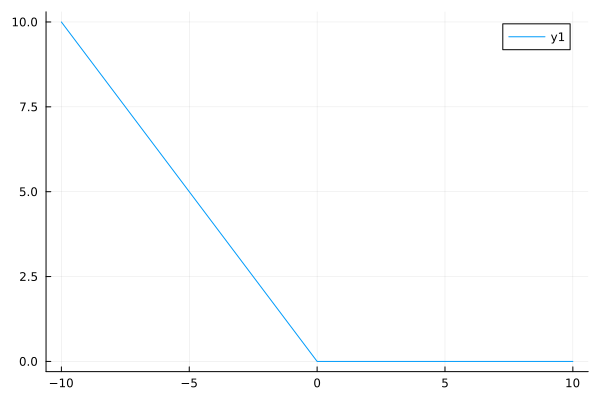
# Smooth max function
../_images/54194a3dd073793db32301862439a1fff4456c2ab4e303d4e7c41c9d4d23f387.png

Approximate max(0, x)

function smoothmax(x; c=(1//2)^10)
    0.5 * (x + smoothabs(x; c))
end

plot(smoothmax, -10, 10)
../_images/6dde891ffc31f454ed1d5e15a76138c48523f6adcf408d2dc3fd2ca6c06309a8.png

Smooth minimal function#

Approximate min(0, x)

function smoothmin(x; c=(1//2)^10)
    0.5 * (smoothabs(x;c) - x)
end

plot(smoothmin, -10, 10)
../_images/8ac9a6758c630cc1cc3d1b2ddb4c3edf6a27dc4d04f1c23598f959e8031a87de.png

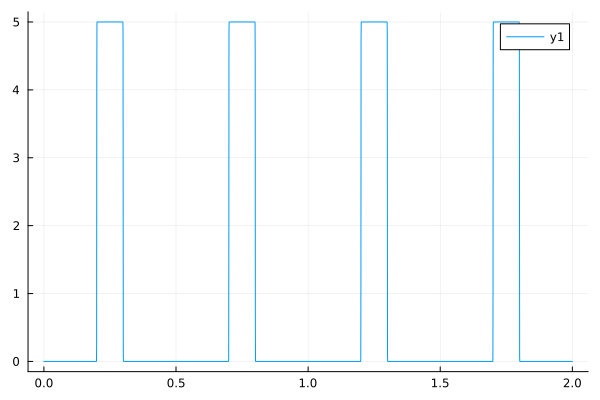
Periodic pulses#

From: https://www.noamross.net/2015/11/12/a-smooth-differentiable-pulse-function/

function smoothpulses(t, tstart, tend, period=1, amplitude=period / (tend - tstart), steepness=1000)
    @assert tstart < tend < period
    xi = 3 / 4 - (tend - tstart) / (2 * period)
    p = inv(1 + exp(steepness * (sinpi(2 * ((t - tstart) / period + xi)) - sinpi(2 * xi))))
    return amplitude * p
end

plot(t->smoothpulses(t, 0.2, 0.3, 0.5), 0.0, 2.0)
../_images/99eacfe4d95d6b75a7b78b673c66e019fcc15739c30c5e2dafcecaea687775d5.png

This notebook was generated using Literate.jl.

Contents