Event-driven continuous-time multiagent model

Event-driven continuous-time multiagent model#

The spatial rock-paper-scissors (RPS) is an ABM with the following rules:

  • Agents can be any of three “kinds”: Rock, Paper, or Scissors.

  • Agents live in a 2D periodic grid space allowing only one agent per cell.

  • When an agent activates, it can do one of three actions:

    1. Attack: choose a random nearby agent and attack it. If the agent loses the RPS game it gets removed.

    2. Move: choose a random nearby position. If it is empty move to it, otherwise swap positions with the agent there.

    3. Reproduce: choose a random empty nearby position (if any exist). Generate there a new agent of the same type.

using Agents
using Random
using LinearAlgebra
using Base64
using Agents.DataFrames
using CairoMakie
CairoMakie.activate!(px_per_unit = 1.0)

Update message: Agents v6

This is a new major version of Agents.jl with lots of cool stuff!
However, from this version onwards, we will stop posting update messages
to the REPL console!

If you want to be updated, follow this discourse post:

https://discourse.julialang.org/t/agents-jl-v6-releases-announcement-post/111678

(and see the CHANGELOG.md file online for a list of changes!)

The helper function is adapted from Agents.abmvideo and correctly displays animations in Jupyter notebooks

function abmvio(model;
    dt = 1, framerate = 30, frames = 300, title = "", showstep = true,
    figure = (size = (600, 600),), axis = NamedTuple(),
    recordkwargs = (compression = 23, format ="mp4"), kwargs...
)
    # title and steps
    abmtime_obs = Observable(abmtime(model))
    if title ≠ "" && showstep
        t = lift(x -> title*", time = "*string(x), abmtime_obs)
    elseif showstep
        t = lift(x -> "time = "*string(x), abmtime_obs)
    else
        t = title
    end

    axis = (title = t, titlealign = :left, axis...)
    # First frame
    fig, ax, abmobs = abmplot(model; add_controls = false, warn_deprecation = false, figure, axis, kwargs...)
    resize_to_layout!(fig)
    # Animation
    Makie.Record(fig; framerate, recordkwargs...) do io
        for j in 1:frames-1
            recordframe!(io)
            Agents.step!(abmobs, dt)
            abmtime_obs[] = abmtime(model)
        end
        recordframe!(io)
    end
end

abmvio (generic function with 1 method)

Define rock, paper, and scissors (RPS) agents. One can use variant(agent) to see the agent type.

@agent struct Rock(GridAgent{2}) end
@agent struct Paper(GridAgent{2}) end
@agent struct Scissors(GridAgent{2}) end
@multiagent RPS(Rock, Paper, Scissors)

Agent actions

function attack!(agent, model)
    # Randomly pick a nearby agent
    contender = random_nearby_agent(agent, model)
    isnothing(contender) && return # do nothing if there isn't anyone nearby
    # The attacking action will be dispatched to the following methods.
    attack!(variant(agent), variant(contender), contender, model)
    return nothing
end

attack!(::AbstractAgent, ::AbstractAgent, contender, model) = nothing
attack!(::Rock, ::Scissors, contender, model) = remove_agent!(contender, model)
attack!(::Scissors, ::Paper, contender, model) = remove_agent!(contender, model)
attack!(::Paper, ::Rock, contender, model) = remove_agent!(contender, model)

attack! (generic function with 5 methods)

Move actions use move_agent! and swap_agents! functions

function move!(agent, model)
    rand_pos = random_nearby_position(agent.pos, model)
    if isempty(rand_pos, model)
        move_agent!(agent, rand_pos, model)
    else
        occupant_id = id_in_position(rand_pos, model)
        occupant = model[occupant_id]
        swap_agents!(agent, occupant, model)
    end
    return nothing
end

move! (generic function with 1 method)

Reproduce actions use replicate! function

function reproduce!(agent, model)
    pos = random_nearby_position(agent, model, 1, pos -> isempty(pos, model))
    isnothing(pos) && return
    # pass target position as a keyword argument
    replicate!(agent, model; pos)
    return nothing
end

reproduce! (generic function with 1 method)

Defining the propensity (“rate” in Gillespie stochastic simulations) and timing of the events

attack_propensity = 1.0
movement_propensity = 0.5
reproduction_propensity(agent, model) = cos(abmtime(model))^2

reproduction_propensity (generic function with 1 method)

Register events with AgentEvent

attack_event = AgentEvent(action! = attack!, propensity = attack_propensity)
reproduction_event = AgentEvent(action! = reproduce!, propensity = reproduction_propensity)

Agents.AgentEvent{typeof(Main.var"##230".reproduce!), typeof(Main.var"##230".reproduction_propensity), DataType, typeof(Agents.exp_propensity)}(Main.var"##230".reproduce!, Main.var"##230".reproduction_propensity, Agents.AbstractAgent, Agents.exp_propensity)

We want a different distribution other than exponential distribution for movement time

function movement_time(agent, model, propensity)
    # Make time around 1
    t = 0.1 * randn(abmrng(model)) + 1
    return clamp(t, 0, Inf)
end

movement_time (generic function with 1 method)

Also rocks do not move

movement_event = AgentEvent(
    action! = move!, propensity = movement_propensity,
    types = Union{Scissors, Paper}, timing = movement_time
)

Agents.AgentEvent{typeof(Main.var"##230".move!), Float64, Union, typeof(Main.var"##230".movement_time)}(Main.var"##230".move!, 0.5, Union{Main.var"##230".Paper, Main.var"##230".Scissors}, Main.var"##230".movement_time)

Collect all events

events = (attack_event, reproduction_event, movement_event)

(Agents.AgentEvent{typeof(Main.var"##230".attack!), Float64, DataType, typeof(Agents.exp_propensity)}(Main.var"##230".attack!, 1.0, Agents.AbstractAgent, Agents.exp_propensity), Agents.AgentEvent{typeof(Main.var"##230".reproduce!), typeof(Main.var"##230".reproduction_propensity), DataType, typeof(Agents.exp_propensity)}(Main.var"##230".reproduce!, Main.var"##230".reproduction_propensity, Agents.AbstractAgent, Agents.exp_propensity), Agents.AgentEvent{typeof(Main.var"##230".move!), Float64, Union, typeof(Main.var"##230".movement_time)}(Main.var"##230".move!, 0.5, Union{Main.var"##230".Paper, Main.var"##230".Scissors}, Main.var"##230".movement_time))

Model function EventQueueABM for an event-driven ABM

const alltypes = (Rock, Paper, Scissors)

function initialize_rps(; n = 100, nx = n, ny = n, seed = 42)
    space = GridSpaceSingle((nx, ny))
    rng = Xoshiro(seed)
    model = EventQueueABM(RPS, events, space; rng, warn = false)
    for p in positions(model)
        # Randomly assign one of the agent
        type = rand(abmrng(model), alltypes)
        add_agent!(p, constructor(RPS, type), model)
    end
    return model
end

initialize_rps (generic function with 1 method)

Have a look at the event queue

model = initialize_rps()
abmqueue(model)

DataStructures.BinaryHeap{Pair{Tuple{Int64, Int64}, Float64}, Base.Order.By{typeof(last), DataStructures.FasterForward}}(Base.Order.By{typeof(last), DataStructures.FasterForward}(last, DataStructures.FasterForward()), [(6080, 1) => 2.9790681020079457e-6, (3987, 1) => 0.0003364593569030146, (6221, 2) => 0.0004887948187761659, (8424, 1) => 0.0006778319693496694, (5035, 1) => 0.0012044922191219774, (7014, 2) => 0.0005771225059120387, (3301, 2) => 0.0011396494447446436, (2505, 1) => 0.0014309955844005063, (5041, 2) => 0.001449028423933035, (5539, 2) => 0.0024520873429744127  …  (9990, 1) => 1.0666363792018059, (9992, 2) => 0.7429399475482082, (9993, 1) => 1.9378465659189394, (4997, 1) => 1.7907183401427267, (2496, 1) => 0.5304394096759053, (2499, 1) => 2.7442278746073216, (4998, 3) => 1.0804360033507288, (4999, 1) => 5.80807081086072, (9998, 1) => 0.9433255253597445, (1250, 3) => 1.258669914970242])

The time in EventQueueABM is continuous, so we can pass real-valued time.

step!(model, 123.456)
nagents(model)

9716

The step! function also accepts a terminating condition.

function terminate(model, t)
    willterm = length(allagents(model)) < 5000
    return willterm || (t > 1000.0)
end

model = initialize_rps()
step!(model, terminate)
abmtime(model)

1000.0000727740552

Data collection#

  • adata: aggregated data to extract information from the execution stats

  • adf: agent data frame

model = initialize_rps()
adata = [(a -> variantof(a) === X, count) for X in alltypes]

adf, mdf = run!(model, 100.0; adata, when = 0.5, dt = 0.01)
adf[1:10, :]
10×4 DataFrame
Rowtimecount_#23_X=Main.var"##230".Rockcount_#23_X=Main.var"##230".Papercount_#23_X=Main.var"##230".Scissors
Float64Int64Int64Int64
10.0329333723335
20.5322632623156
31.0326632023002
41.5318431092839
52.0309329872644
62.51295928792421
73.02293428492288
83.53306829682348
94.04322130342392
104.55325130582358

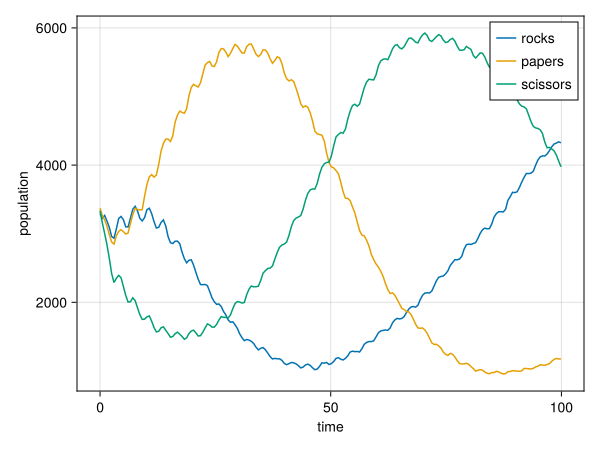
Visualize population change#

tvec = adf[!, :time]  ## time as x axis
populations = adf[:, Not(:time)]  ## agents as data
alabels = ["rocks", "papers", "scissors"]

fig = Figure();
ax = Axis(fig[1,1]; xlabel = "time", ylabel = "population")
for (i, l) in enumerate(alabels)
    lines!(ax, tvec, populations[!, i]; label = l)
end
axislegend(ax)
fig
_images/b561509780ff15eb3a83e15dc22cdfd664c49f97f81983a8542b3478af30a5d7.png

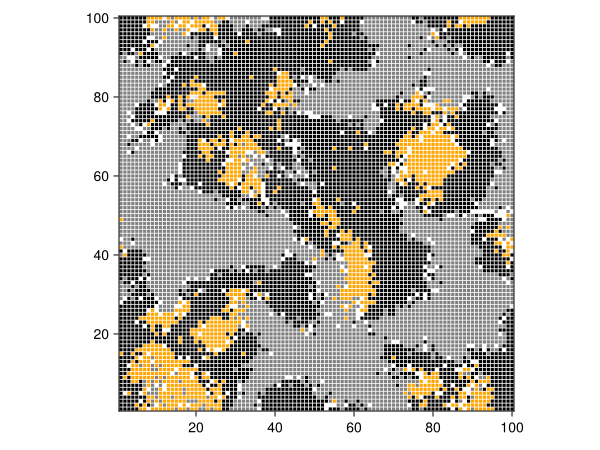
Visualize agent distribution#

const colormap = Dict(Rock => "black", Scissors => "gray", Paper => "orange")
agent_color(agent) = colormap[variantof(agent)]
plotkw = (agent_color, agent_marker = :rect, agent_size = 5)
fig, ax, abmobs = abmplot(model; plotkw...)

fig
_images/f3bc23028bf58388a4ffc63e6a5c476de1a5246b27930ceaf91c13e1f532436d.png

Animation#

model = initialize_rps()
vio = abmvio( model;
    dt = 0.5, frames = 300,
    title = "Rock Paper Scissors (event based)",
    plotkw...,
)

save("rps.mp4", vio)
vio |> display

This notebook was generated using Literate.jl.