2D time-independent heat equation#
From the tutorial
Using MethodOfLines.jl (SciML/MethodOfLines.jl) to symbolically define the PDE system and use the finite difference method (FDM) to solve the following PDE:
\[
\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}
\]
using ModelingToolkit
using MethodOfLines
using DomainSets
using OrdinaryDiffEq
using NonlinearSolve
using Plots
Setup variables and differential operators
@independent_variables x y
@variables u(..)
Dxx = Differential(x)^2
Dyy = Differential(y)^2
Differential(y) ∘ Differential(y)
PDE equation
eq = Dxx(u(x, y)) + Dyy(u(x, y)) ~ 0
\[ \begin{equation}
\frac{\mathrm{d}}{\mathrm{d}y} \frac{\mathrm{d}}{\mathrm{d}y} u\left( x, y \right) + \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} u\left( x, y \right) = 0
\end{equation}
\]
Boundary conditions
bcs = [u(0, y) ~ x * y,
u(1, y) ~ x * y,
u(x, 0) ~ x * y,
u(x, 1) ~ x * y
]
\[\begin{split} \begin{align}
u\left( 0, y \right) &= x y \\
u\left( 1, y \right) &= x y \\
u\left( x, 0 \right) &= x y \\
u\left( x, 1 \right) &= x y
\end{align}
\end{split}\]
Space and time domains
domains = [ x ∈ Interval(0.0, 1.0), y ∈ Interval(0.0, 1.0)]
2-element Vector{Symbolics.VarDomainPairing}:
Symbolics.VarDomainPairing(x, 0.0 .. 1.0)
Symbolics.VarDomainPairing(y, 0.0 .. 1.0)
PDE system
@named pdesys = PDESystem(eq, bcs, domains, [x, y], [u(x, y)])
\[ \begin{align}
\frac{\mathrm{d}}{\mathrm{d}y} \frac{\mathrm{d}}{\mathrm{d}y} u\left( x, y \right) + \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} u\left( x, y \right) &= 0
\end{align}
\]
Discretize the PDE system into an Nonlinear system
Pass nothing to the time parameter
@time prob = let dx=0.1
discretization = MOLFiniteDifference([x=>dx, y=>dx], nothing, approx_order=2, grid_align = MethodOfLines.EdgeAlignedGrid())
prob = discretize(pdesys, discretization)
end
23.101843 seconds (46.13 M allocations: 2.209 GiB, 2.23% gc time, 94.90% compilation time: 21% of which was recompilation)
NonlinearProblem with uType Vector{Float64}. In-place: true
u0: 25-element Vector{Float64}:
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
⋮
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
Solve the PDE
@time sol = NonlinearSolve.solve(prob, NewtonRaphson())
18.502082 seconds (45.73 M allocations: 1.906 GiB, 5.00% gc time, 82.30% compilation time)
retcode: Stalled
Interpolation: Dict{Symbolics.Num, Interpolations.GriddedInterpolation{Float64, 2, Matrix{Float64}, Interpolations.Gridded{Interpolations.Linear{Interpolations.Throw{Interpolations.OnGrid}}}, Tuple{Vector{Float64}, Vector{Float64}}}}
ivs: 2-element Vector{SymbolicUtils.BasicSymbolic{Real}}:
y
xdomain:(-0.05:0.1:1.05, -0.05:0.1:1.05)
u: Dict{Symbolics.Num, Matrix{Float64}} with 1 entry:
u(x, y) => [0.0 -0.0025006 … -0.0474763 0.0; -0.00250061 0.0025006 … 0.047504…
Extract data
discrete_x = sol[x]
discrete_y = sol[y]
u_sol = sol[u(x,y)]
12×12 Matrix{Float64}:
0.0 -0.0025006 -0.00750183 … -0.0425273 -0.0474763 0.0
-0.00250061 0.0025006 0.00750183 0.0425111 0.0475042 0.0524969
-0.00750179 0.00750179 0.0225054 0.127513 0.142485 0.157404
-0.0125029 0.0125029 0.0375089 0.212534 0.23752 0.262465
-0.0175039 0.0175039 0.052512 0.297562 0.332596 0.367768
-0.0225046 0.0225046 0.0675143 … 0.382548 0.427535 0.472356
-0.027505 0.027505 0.0825155 0.467488 0.522639 0.580171
-0.0325048 0.0325048 0.097515 0.552041 0.615363 0.673049
-0.037504 0.037504 0.112513 0.637818 0.713722 0.790437
-0.0425027 0.0425027 0.127508 0.722872 0.811269 0.905719
-0.0475009 0.0475009 0.142503 … 0.804809 0.902765 0.997466
0.0 0.0524991 0.157497 0.881458 0.997516 0.0
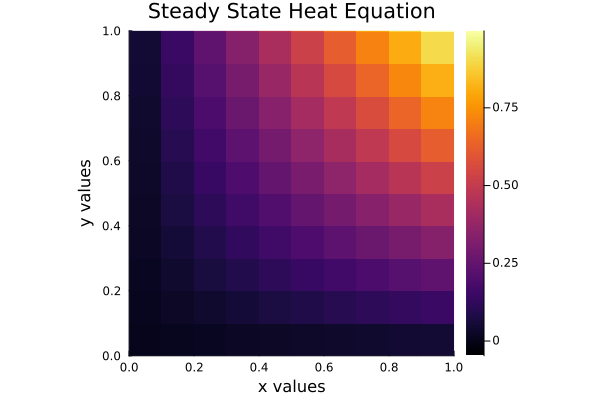
Visualize the solution
heatmap(
discrete_x, discrete_y, u_sol,
xlabel="x values", ylabel="y values", aspect_ratio=:equal,
title="Steady State Heat Equation", xlims=(0, 1), ylims=(0, 1)
)
This notebook was generated using Literate.jl.