1D PDE: SIS diffusion model

Source

\[\begin{split} \begin{align} \frac{\partial S}{\partial t} &= d_S S_{xx} - \beta(x)\frac{SI}{S+I} + \gamma(x)I \\ \frac{\partial I}{\partial t} &= d_I I_{xx} + \beta(x)\frac{SI}{S+I} - \gamma(x)I \end{align} \end{split}\]

where \(x \in (0, 1)\)

Solve the steady-state problem \(\frac{\partial S}{\partial t} = \frac{\partial I}{\partial t} = 0\)

The boundary condition: \(\frac{\partial S}{\partial x} = \frac{\partial I}{\partial x} = 0\) for x = 0, 1

The conservative relationship: \(\int^{1}_{0} (S(x) + I(x) ) dx = 1\)

Notations:

• \(x\) : location

• \(t\) : time

• \(S(x, t)\) : the density of susceptible populations

• \(I(x, t)\) : the density of infected populations

• \(d_S\) / \(d_I\) : the diffusion coefficients for susceptible and infected individuals

• \(\beta(x)\) : transmission rates

• \(\gamma(x)\) : recovery rates

using OrdinaryDiffEq
using ModelingToolkit
using MethodOfLines
using DomainSets
using Plots

Setup parameters, variables, and differential operators

@parameters t x
@parameters dS dI brn ϵ
@variables S(..) I(..)
Dt = Differential(t)
Dx = Differential(x)
Dxx = Differential(x)^2

Differential(x) ∘ Differential(x)

Helper functions

γ(x) = x + 1
ratio(x, brn, ϵ) = brn + ϵ * sinpi(2x)

ratio (generic function with 1 method)

1D PDE for disease spreading

eqs = [
    Dt(S(t, x)) ~ dS * Dxx(S(t, x)) - ratio(x, brn, ϵ) * γ(x) * S(t, x) * I(t, x) / (S(t, x) + I(t, x)) + γ(x) * I(t, x),
    Dt(I(t, x)) ~ dI * Dxx(I(t, x)) + ratio(x, brn, ϵ) * γ(x) * S(t, x) * I(t, x) / (S(t, x) + I(t, x)) - γ(x) * I(t, x)
]

\[\begin{split} \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} S\left( t, x \right) &= \frac{ - \left( 1 + x \right) S\left( t, x \right) I\left( t, x \right) \left( \mathtt{brn} + sinpi\left( 2 x \right) \epsilon \right)}{S\left( t, x \right) + I\left( t, x \right)} + \mathtt{dS} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} S\left( t, x \right) + \left( 1 + x \right) I\left( t, x \right) \\ \frac{\mathrm{d}}{\mathrm{d}t} I\left( t, x \right) &= \frac{\left( 1 + x \right) S\left( t, x \right) I\left( t, x \right) \left( \mathtt{brn} + sinpi\left( 2 x \right) \epsilon \right)}{S\left( t, x \right) + I\left( t, x \right)} + \mathtt{dI} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} I\left( t, x \right) - \left( 1 + x \right) I\left( t, x \right) \end{align} \end{split}\]

Boundary conditions

bcs = [
    S(0, x) ~ 0.9 + 0.1 * sinpi(2x),
    I(0, x) ~ 0.1 + 0.1 * cospi(2x),
    Dx(S(t, 0)) ~ 0.0,
    Dx(S(t, 1)) ~ 0.0,
    Dx(I(t, 0)) ~ 0.0,
    Dx(I(t, 1)) ~ 0.0
]

\[\begin{split} \begin{align} S\left( 0, x \right) &= 0.9 + 0.1 sinpi\left( 2 x \right) \\ I\left( 0, x \right) &= 0.1 + 0.1 cospi\left( 2 x \right) \\ \frac{\mathrm{d}}{\mathrm{d}x} S\left( t, 0 \right) &= 0 \\ \frac{\mathrm{d}}{\mathrm{d}x} S\left( t, 1 \right) &= 0 \\ \frac{\mathrm{d}}{\mathrm{d}x} I\left( t, 0 \right) &= 0 \\ \frac{\mathrm{d}}{\mathrm{d}x} I\left( t, 1 \right) &= 0 \end{align} \end{split}\]

Space and time domains

domains = [
    t ∈ Interval(0.0, 10.0),
    x ∈ Interval(0.0, 1.0)
]

2-element Vector{Symbolics.VarDomainPairing}:
 Symbolics.VarDomainPairing(t, 0.0 .. 10.0)
 Symbolics.VarDomainPairing(x, 0.0 .. 1.0)

Build the PDE system

@named pdesys = PDESystem(eqs, bcs, domains,
    [t, x], ## Independent variables
    [S(t, x), I(t, x)],  ## Dependent variables
    [dS, dI, brn, ϵ],    ## parameters
    defaults = Dict(dS => 0.5, dI => 0.1, brn => 3, ϵ => 0.1)
)

\[\begin{split} \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} S\left( t, x \right) &= \frac{ - \left( 1 + x \right) S\left( t, x \right) I\left( t, x \right) \left( \mathtt{brn} + sinpi\left( 2 x \right) \epsilon \right)}{S\left( t, x \right) + I\left( t, x \right)} + \mathtt{dS} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} S\left( t, x \right) + \left( 1 + x \right) I\left( t, x \right) \\ \frac{\mathrm{d}}{\mathrm{d}t} I\left( t, x \right) &= \frac{\left( 1 + x \right) S\left( t, x \right) I\left( t, x \right) \left( \mathtt{brn} + sinpi\left( 2 x \right) \epsilon \right)}{S\left( t, x \right) + I\left( t, x \right)} + \mathtt{dI} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} I\left( t, x \right) - \left( 1 + x \right) I\left( t, x \right) \end{align} \end{split}\]

Finite difference method (FDM) converts the PDE system into an ODE problem

dx = 0.01
order = 2
discretization = MOLFiniteDifference([x => dx], t, approx_order=order)
prob = discretize(pdesys, discretization)

ODEProblem with uType Vector{Float64} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (0.0, 10.0)
u0: 198-element Vector{Float64}:
 0.19980267284282716
 0.1992114701314478
 0.19822872507286887
 0.1968583161128631
 0.19510565162951538
 0.19297764858882513
 0.190482705246602
 0.18763066800438638
 0.18443279255020154
 0.18090169943749476
 ⋮
 0.9535826794978997
 0.9481753674101716
 0.9425779291565073
 0.9368124552684678
 0.9309016994374948
 0.9248689887164855
 0.9187381314585725
 0.9125333233564304
 0.9062790519529313

Solving time-dependent SIS epidemic model

KenCarp4 is good at solving semilinear problems (like reaction-diffusion problems).

sol = solve(prob, KenCarp4(), saveat=0.2)

retcode: Success
Interpolation: Dict{Symbolics.Num, Interpolations.GriddedInterpolation{Float64, 2, Matrix{Float64}, Interpolations.Gridded{Interpolations.Linear{Interpolations.Throw{Interpolations.OnGrid}}}, Tuple{Vector{Float64}, Vector{Float64}}}}
t: 51-element Vector{Float64}:
  0.0
  0.2
  0.4
  0.6
  0.8
  1.0
  1.2
  1.4
  1.6
  1.8
  ⋮
  8.4
  8.6
  8.8
  9.0
  9.2
  9.4
  9.6
  9.8
 10.0ivs: 2-element Vector{SymbolicUtils.BasicSymbolic{Real}}:
 t
 xdomain:([0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8  …  8.2, 8.4, 8.6, 8.8, 9.0, 9.2, 9.4, 9.6, 9.8, 10.0], 0.0:0.01:1.0)
u: Dict{Symbolics.Num, Matrix{Float64}} with 2 entries:
  S(t, x) => [0.904194 0.906279 … 0.893721 0.895806; 0.879603 0.879585 … 0.7899…
  I(t, x) => [0.2 0.199803 … 0.199803 0.2; 0.204066 0.20397 … 0.245398 0.245559…

Grid points

discrete_x = sol[x]
discrete_t = sol[t]

51-element Vector{Float64}:
  0.0
  0.2
  0.4
  0.6
  0.8
  1.0
  1.2
  1.4
  1.6
  1.8
  ⋮
  8.4
  8.6
  8.8
  9.0
  9.2
  9.4
  9.6
  9.8
 10.0

Results (Matrices)

S_solution = sol[S(t, x)]
I_solution = sol[I(t, x)]

51×101 Matrix{Float64}:
 0.2       0.199803  0.199211  0.198229  …  0.199211  0.199803  0.2
 0.204066  0.20397   0.203684  0.203205     0.244914  0.245398  0.245559
 0.239603  0.239568  0.239463  0.239285     0.320347  0.320719  0.320844
 0.300269  0.300279  0.300309  0.300355     0.413565  0.413853  0.413949
 0.37595   0.375987  0.376098  0.376278     0.503721  0.503946  0.504021
 0.451583  0.451629  0.451768  0.451996  …  0.573511  0.573687  0.573745
 0.516804  0.516848  0.516981  0.517198     0.620077  0.620214  0.62026
 0.566319  0.566357  0.566469  0.566653     0.646894  0.647002  0.647038
 0.601149  0.601179  0.601268  0.601415     0.660188  0.660274  0.660303
 0.624958  0.624981  0.625051  0.625165     0.665471  0.665541  0.665564
 ⋮                                       ⋱                      ⋮
 0.676304  0.676307  0.676318  0.676335     0.656519  0.656544  0.656553
 0.676303  0.676307  0.676318  0.676335     0.656519  0.656544  0.656553
 0.676303  0.676307  0.676317  0.676334     0.656519  0.656544  0.656553
 0.676302  0.676306  0.676317  0.676333  …  0.656519  0.656545  0.656553
 0.676301  0.676305  0.676316  0.676333     0.65652   0.656545  0.656554
 0.676301  0.676304  0.676315  0.676332     0.65652   0.656546  0.656554
 0.6763    0.676304  0.676315  0.676331     0.656521  0.656546  0.656554
 0.6763    0.676304  0.676314  0.676331     0.656521  0.656546  0.656554
 0.6763    0.676304  0.676315  0.676331  …  0.656521  0.656546  0.656554

Visualize the solution

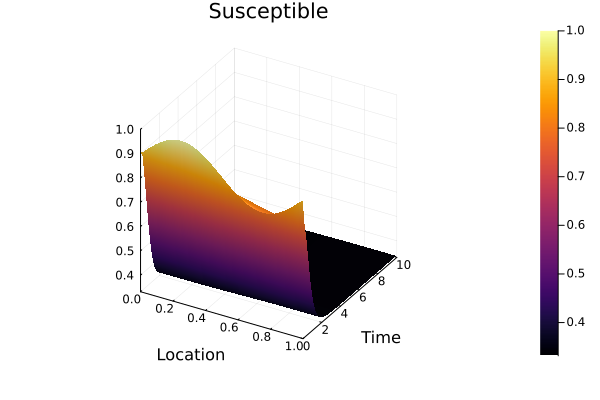
surface(discrete_x, discrete_t, S_solution, xlabel="Location", ylabel="Time", title="Susceptible")

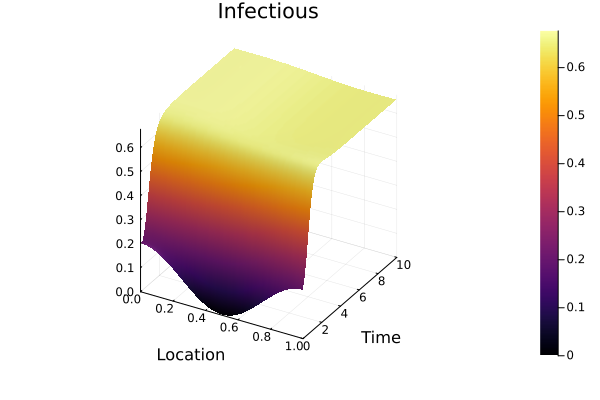
surface(discrete_x, discrete_t, I_solution, xlabel="Location", ylabel="Time", title="Infectious")

---

This notebook was generated using Literate.jl.