Applied electricity

Course notes of Applied electricity by Lecturer 林冠中.

Course information¶

Lecturer: 林冠中 (calculus365(at)yahoo.com.tw)
Time: Fri. ABCD
Location: EE1-201 Lab
Office hour (please make a reservation by email):
Mon. 5 pm
Tue. evening
Fri. after class

TL;DR¶

SI units for electrical circuits:
time(t): second
current(i): Ampere
voltage(v): Volt
resistance(r): Ohm
power(p): Watt
SI prefixes
Directionality matters. Negative sign = opposite direction
Minus to plus: voltage gain; plus to minus voltage drop
Ohm's Law: V = IR
Kirchhoff's circuit laws
KCL : $Σi_{in} = Σi_{out}$ (on a node)
KVL : $ΣV_{drop} = ΣV_{supply}$ (around a loop)
Power: $P = IV$

Current¶

Flow of positive charge versus time: $i(t) = \frac{dq}{dt}$
1 Ampere = 1 Coulomb per second

Voltage¶

Change in energy (in Joules) from moving 1 Coulomb of charge
1 Volt = 1 Joule change per Coulomb: $V = \frac{Q}{C}$
Change in electrical potential ($φA - φB$)
Ground: V = 0 (manually set)
$V_{ab} = V_{a} - V_{b}$
Power supplier (source): pointing from minus (-) to plus (+)
Power receiver (load): pointing from plus (+) to minus (-)

Dependent sources¶

Find where the depending parameter is and note the units. Wikipedia

Power balance¶

Rule of thumb: supply = load. Beware directionality of both current and voltage across a device.

Resistive circuits, Nodal and mesh analysis¶

Conductance G = 1/R, Unit: Siemens (S)
Short circuit: V = 0, R = 0
Open circuit: I = 0, G = 0
Passive component: R >= 0
Parallel circuit: same voltage
Serial circuit: same current

Nodal analysis¶

Use Kirchhoff's current laws (current in = current out)
Grounding (set V = 0) on one of the node.
Super-node (Voltage source): direct voltage difference between nodes, reducing the need to find currents

Loop (mesh) analysis¶

Use Kirchhoff's voltage laws (voltage supplied = voltage consumed)
Note that currents add up in common sides of the loops.
Super-mesh (Current source): direct current inference in the loop.

Series / parallel circuits¶

Serial: one common point. $R_s = R_1 + R_2$
Parallel: two common points. $R_p = \frac{R_1R_2}{R_1 + R_2}$
Analysis: combining resistors bottom-up.
Voltage divider: series resistors
Current divider: parallel resistors

Resistor tolerance¶

Last colored ring on the resistor.
Need to design some room for the components according to the tolerance (min and max values)

Y-Δ transformation¶

https://en.wikipedia.org/wiki/Y-%CE%94_transform

Δ -> Y: denominator = sum of the three; numerator = product of the twos next to the node
Y -> Δ: denominator = the opposite one; numerator = sum of products of two
Electric bridge balance: products of the opposite sides are the same
central current = 0 => equivalent to open circuit

Question¶

What is the difference between node and loop analysis?

The principle of superposition¶

Effects of multiple sources could be added (superposition) individually.
Remove voltage source = short circuit
Remove current source = open circuit

Thevenin and Norton equivalent circuits¶

Thévenin's theorem

Simplifying circuit in a black box from the principle of superposition
Find equivalent resistance ($R_{TH}$) after source removal.
Find equivalent open circuit voltage (source) for Thevenin's theorem
Or, find equivalent short circuit current (source) for Norton's theorem

For dependent sources¶

Pure dependent sources cannot self-start: $V_{TH}$ = 0
Finding $R_{TH}$ requires a probe source: $R_{TH} = {V_p}/{I_p}$
I_p : short circuit current with a probe source
Like one would do in a an circuit experiment

Maximum power transfer¶

When $R_{Load} = R_{TH}$, the power is maximum $P = V_{TH}^2 / (4R_{TH}) $

Norton's theorem¶

$R_{TH}$ the same as Thevenin
$I_{SC}$ : short circuit current instead of open circuit voltage
$I_{SC} = V_{OC} / R_{TH}$

Capacitors and Capacitance¶

$i = C \frac{dV}{dt}$
Smooth voltage change
At t=0 and uncharged: short-circuit
DC steady-state: open-circuit
Energy stored: $0.5CV^2$
Series / Parallel: opposite to resistors

Inductors and Inductance¶

$v = L \frac{di}{dt}$
Smooth current change
At t=0 and no mag. flux: open-circuit
DC steady-state: short-circuit
Energy stored: $0.5Li^2$
Series / Parallel: the same as resistors

AC steady-state analysis¶

Periodic signal: $x(t) = x(t + nT)$
Sinusoidal waveform: $x(t) = Acos(\omega t + \phi)$
$\omega = 2\pi f$
$f = 1/T$
$2\pi$ rad = 360 degrees

RMS (Root mean square), effective value¶

Peak = $\sqrt{2}$ RMS value for sinusoidal current and voltage.

Phase lead / lag¶

Leads by 45 degrees: $x(t) = Acos(\omega t + 45^o)$
Lags by 45 degrees: $x(t) = Acos(\omega t - 45^o)$
Pure capacitor + AC circuit: current leads voltage by 90 degrees
Pure inductor + AC circuit: current lags voltage by 90 degrees

Complex algebra¶

Euler's formula: $e^{j\theta} = cos(\theta) + sin(\theta)$
Frequency term ($e^{j\omega t}$) is usually omitted in favor of angle notation.
Multiplication: angle addition; division: angle subtraction for waveforms of the same freq.

Impedance¶

Generalization to resistance in the complex domain
The same way in calculations as that in the case of resistance
Admittance: Generalization to conductance (reciprocal of impedance)
Inductor: $Z_{L} = j\omega L$
Capacitor: $Z_{C} = 1/(j\omega C)$
Impedance is frequency-dependent. Higher freq: higher impedance from inductors; lower freq: higher impedance from capacitors

Filter¶

Proved from impedance analysis
Frequency response: transfer function = gain function
Low pass filter: the RC circuit
Bode plot: x: input frequency (log scale), y: response (amplitude)

RC, RL, and RLC circuits¶

First, convert it to the equivalent circuit (Thevenin) for further analysis
Time constants may be different in charging / discharging due to different circuits

RC transients¶

Voltage is continuous, while current is not.
For uncharged capacitor, initial voltage across the capacitor is zero (i.e. short circuit)
when charging, it approaches applied voltage. The steady-state is open circuit.
Discharging: positive voltage and negative current.
Time scale $\tau_{C} = RC$
Charging transient: $v_{C} = E - i_{C}R$, $i_{C} = \frac{E}{R}e^{-t/\tau_{C}}$
Discharging transient: $v_{C} = V_0e^{-t/\tau_{C}}$, $i_{C} = -v_{C}/ R$
$t/\tau_{C} > 5$: > 99% completed charging / discharging

RL transient¶

Current is continuous, while voltage is not.
For uncharged inductor, initial current is zero (open circuit); then approaches terminal current upon charging. The steady-state is short circuit.
Discharging: positive current and negative voltage (Lenz's law).
Time scale $\tau_{L} = L/R$
Charging transient: $v_{L} = Ee^{-t/\tau_{L}}$, $i_{L} = (E - v_{L}) / R$
Discharging transient: $v_{L} = -I_0Re^{-t/\tau_{L}}$, $i_{L} = I_0e^{-t/\tau_{L}}$

RLC transients¶

Solving series RLC circuit by KVL: $V_R + V_L + V_C = E$
$\frac{d^2I}{dt^2} + \frac{R}{L}\frac{dI}{dt} + \frac{I}{LC} = 0$, due to E is constant (DC)
Let $I = e^{\lambda t}$, $\lambda = \frac{-R}{2L} \plusmn \sqrt{(\frac{R}{2L})^2 - \frac{1}{LC}}$
Resonant frequency: $\omega_0^2 = \frac{1}{LC}$
Solving parallel RLC circuit by KCL: the same resonant frequency: $\omega_0^2 = \frac{1}{LC}$

Damping¶

Overdamping: $(\frac{R}{2L})^2 - \frac{1}{LC} > 0$
Critical damping: $(\frac{R}{2L})^2 - \frac{1}{LC} = 0$ (decaying faster than overdamping)
Underdamping: $(\frac{R}{2L})^2 - \frac{1}{LC} < 0$, oscillation (+)

Quality factor¶

Bandwidth

Wikipedia

At resonance: $Z_{C}$ and $Z_{L}$ cancel each other out
$Q = f_{r} / BW$
BW: Bandwidth
Series RLC: $Q = \frac{1}{R}\sqrt{\frac{L}{C}}$
Parallel RLC: $Q = \frac{R}{1}\sqrt{\frac{C}{L}}$

Steady state power analysis¶

Note and specify the difference between peak values ($I_{M}$, $V_{M}$) and the effective (RMS) values.
$ p = \frac{V_M I_M}{2}(cos(\theta_v - \theta_i) + cos(2\omega t + \theta_v + \theta_i))$
Twice the frequency: $2\omega t$ compared to current and voltage
Average power: $V_M I_M cos(\theta_v - \theta_i)/2 = V_{rms} I_{rms} cos(\theta_v - \theta_i) = P_{app} \cdot pf $
- Apparent power: $P_{app} = V_M I_M / 2 = V_{rms} I_{rms}$
- Power factor: $pf = cos(\theta_v - \theta_i)$. The phase difference between voltage and current
- Purely resistive: $p = V_M I_M / 2 = V_{rms} I_{rms}$. pf = 1
- Purely capacitive / inductive: $p = pf = 0$. Does not absorb power on average.
- For average power, one could calculate the resistive part only.

Maximum power transfer¶

When $Z_{L} = Z_{TH}^*$ , Im(ΣZ)= 0,
$P_{L,max} = 0.5 * \frac{\lvert V_{OC} \rvert\ ^2 }{4 R_{TH}}$ (Since $P = 0.5 V_{M}I_{M}$)

Power factor and complex power¶

$p = V_M I_M cos(\theta_v - \theta_i)/2 = P_{app} \cdot pf$. Unit:VA
Phase difference = 0 (purely resistive), pf = 1
Phase difference = -90 (purely capacitive) or 90 (purely inductive), pf = 0

Active power vs reactive power¶

$S = P_{app} cos(\theta_v - \theta_i) + jP_{app} * sin(\theta_v - \theta_i)$
* Former: active power (P); latter: reactive power (Q)
* $\lvert S \rvert = \sqrt{P^2 + Q^2} = P_{app} = V_{rms} I_{rms}$
* $P = \lvert S \rvert \cdot pf$
* For capacitive circuit: Q < 0; inductive circuit: Q > 0

Safety considerations¶

100 mA to the heart: Ventricular tachycardia and could be fatal
Grounding: increase safety by shunt the current away from the user in case of fault
Ground fault interrupter(GFI):
No fault: In current = out current, do nothing
Fault: If current is not the same as out, it induces current in the sensing coil and breaks the circuit.
Accidental grounding: new path for currents, new hazard.

Magnetically coupled circuits¶

Mutual inductance¶

Open circuit $v_2 = L_{21}\frac{di_1}{dt}$
Two current sources: self inductance plus mutual inductance
$v_1 = L_1\frac{di_1}{dt} + L_{12}\frac{di_2}{dt}$
$v_2 = L_{21}\frac{di_1}{dt} + L_{2}\frac{di_2}{dt}$
Beware the dot (current direction of the input and output): turn them into standard circuit
The linear model states $L_{21} = L_{12} = M$
Mutual inductance in series inductors: $L_{eq} = L_1 + L_2 \pm 2M$
Mutual inductance in parallel inductors: $L_{eq} = \frac{L_1L_2 - M^2}{L_1 + L_2 \mp 2M}$

Energy analysis¶

$w = 0.5L_1I_1^2 + 0.5L_2I_2^2 \pm MI_1I_2$
$M \le \sqrt{L_1L_2}$, the geometric mean of L1 and L2
$k = \frac{M}{\sqrt{L_1L_2}}$, coupling coefficient (0 to 1)

Transformers¶

Iron core, air core, composite core
Ideal transformers: no energy loss (Pin = Pout)
$\frac{V_1}{V_2} = \frac{N_1}{N_2}$
$\frac{i_1}{i_2} = \frac{N_2}{N_1}$
$\frac{Z_1}{Z_2} = (\frac{N_1}{N_2})^2$
Analysis of simple transformer circuits (PhD qualification exam)
Application: AC -> transformer -> rectifier -> filter -> regulator -> DC
Practical transformers
Leakage of magnetic flux
Winding resistance: copper loss
Core loss: eddy current, hysteresis
efficiency: $\eta = \frac{P_{out}}{P_{in}}$

Frequency response¶

Resistive circuit: freq-independent $|Z_R|$ = const, θ = 0
Inductive $|Z_L|\varpropto f$, θ = 90
Capacitive $|Z_C|\varpropto 1/f$, θ = -90

Series RLC¶

$Z_{eq} = R + j\omega L + \frac{1}{j\omega C}$

$|Z_{eq}| = \frac{\sqrt{(\omega RC)^2 + (1-\omega^2LC)^2}}{\omega C}$

Minimal $|Z_{eq}|$ when $\omega = \omega_0 = \frac{1}{\sqrt{LC}}$ (resonant frequency) and $Im(Z_{eq}) = 0$

Bode plot¶

Wikipedia

x-axis: freq (log(f) )
y-axis: magnitude (20*log(M), in dB) / phase (in degrees)
dB is for power amplification / attenuation
dBm = $10log\frac{p}{1mW}$

Multistage system¶

Amplitude: product of all systems
dB: sum of all dB gains

Network transfer function¶

\[ H(s) = \frac{X_{out}(s)}{Y_{in}(s)} \]

Thevenin equivalence theorem for finding the gain.

Bandwidth¶

Dependent on reactive elements (usually RC circuits, inductors are more difficult to handle)

Cutoff frequency: -3dB (0.707x) voltage magnitude (half power)

Quality factor and effective bandwidth¶

Series RLC: $Q = \frac{\omega_0 L}{R} = \frac{1}{R}\sqrt{\frac{L}{C}}$

Bandwidth (BW) = $\omega_0$ / Q = $\omega_{hi} - \omega_{lo}$

$\omega_{hi} \omega_{lo} = \omega_0^2$

Poles and Zeros¶

Let $s = j\omega$ (Laplace transform)

For series RLC:
$Z_{eq} = R + sL + \frac{1}{sC} = \frac{s^2LC + sRC + 1}{sC}$

$H(s) = K_0 \frac{(s-z_1)(s-z_2)...}{(s-p_1)(s-p_2)...}$

$K_0$ : DC term
zeros: H(s) = 0
poles: H(s) diverges

Filters¶

Low-pass <-> high pass by an RC circuit
Band-pass <-> band reject (notch filter) by an RLC circuit or a combination of a low-pass and a high-pass filter

OP-Amp¶

OP-Amp on Wikipedia

Ideal OP-Amp¶

Infinite open-loop gain G = $v_{out} / v_{in}$
Infinite input impedance $R_{in}$, thus zero input current
Zero input offset voltage
Infinite output voltage range, not clipped by supplied voltage
Infinite bandwidth with zero phase shift and infinite slew rate
Zero $R_{out}$, output impedance
Zero noise
Infinite common-mode rejection ratio (CMRR)
Infinite power supply rejection ratio.

Circuit analysis in Ideal OP-Amp¶

$V_{-} \approx V_{+}$
$i_{-+} \approx 0$
Make sure $V_{out}$ is in the range of supplied voltages.

The rest is Ohm's law and circuit analysis.

More OP-Amp circuits¶

Multiple input voltages¶

Principle of superposition. One voltage source at a time.

With energy-storing devices¶

Differentiator
Integrator
Antoniou Inductance Simulation Circuit

$L = C_4 R_1 R_3 R_5 / R_2$

Semiconductors¶

Materials¶

Group IV: Si, Ge
Group III + V: GaN, GaAs(P)

Why semi-conductivity¶

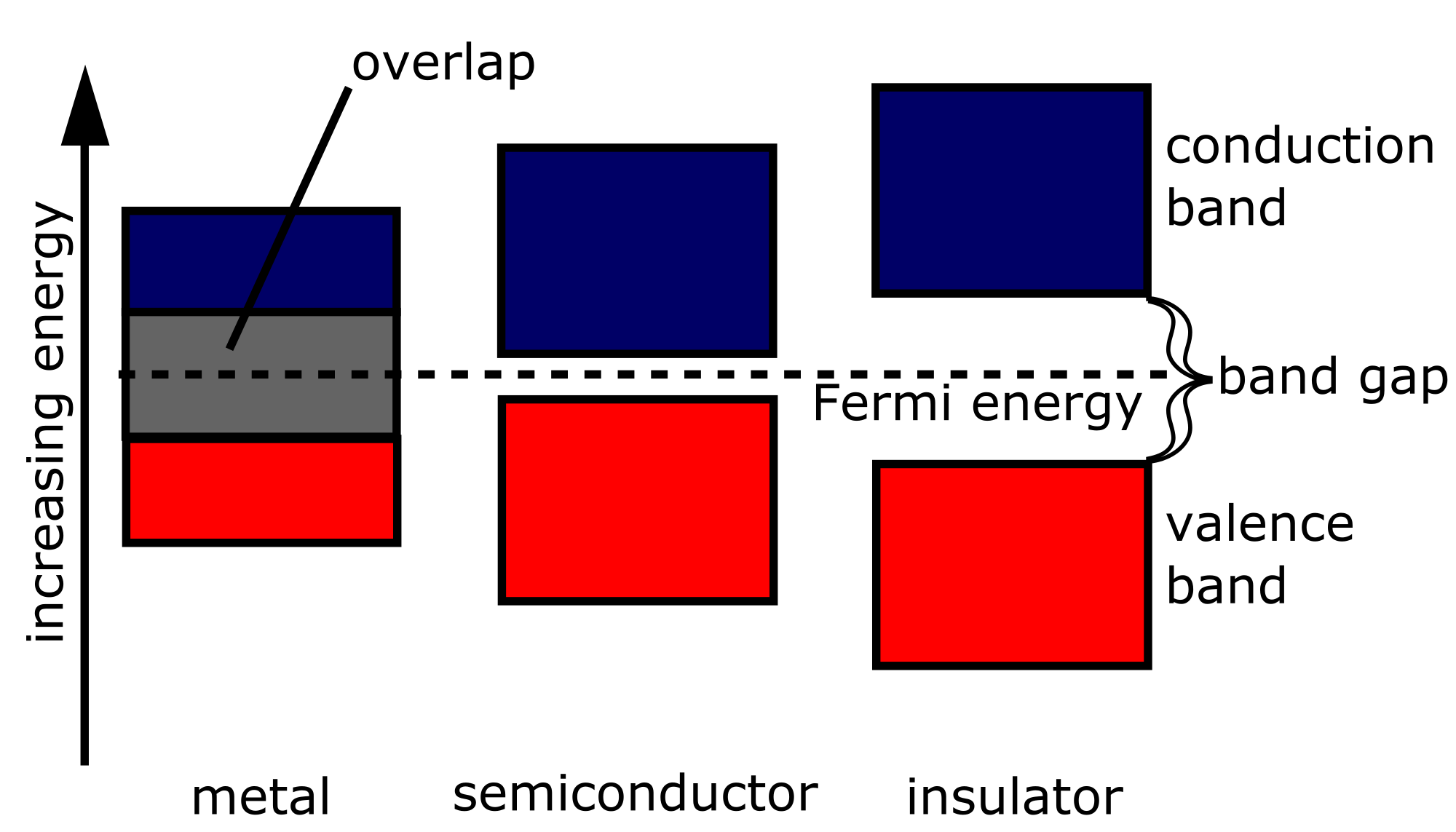
Band gap energy difference $E_{g}$ = $E_{c}$ - $E_{v}$
Insulators: > 5 eV
Semiconductors: smaller gap, a small amount of electrons escape from valence band to the conduction band
Conductors (metal, graphite): overlap (no gap)
Direct (III+V) vs indirect (IV) band gaps
Direct: could emit photons (LED, photo detector)
Indirect: emit a phonon in the crystal
The tetrahedral covalent bond crystalline structure for extrinsic (doped) semiconductors

Carriers¶

Electrons (e-) in the conduction band as well as the vacancies in the valence band (holes, h+)
For intrinsic semiconductors, motility factor $\mu$: GaN (GaAs) >Ge > Si, parallel with conductivity
Enriched by doping (increase both $\mu$ and conductivity): making extrinsic semiconductors
Doping group V elements (donor impurities): electrons are major carriers (N-type)
Doping group III elements (acceptor impurities): holes are major carriers (P-type)
N-type semiconductors have higher $\mu$ than P-type since electrons have lower effective mass than holes. Thus, N-type is better for high-freq applications. But P-type has dual role, being both resistors and semiconductor switches.

P-N junctions and diodes¶

P-N junction

Depletion zone¶

Diffusion of major carriers generate an electric field across the boundary
A zone with little carriers, high resistance
Process a barrier voltage

Applying voltage¶

Forward bias: shrinking depletion zone, high conductivity
Reverse bias: widening depletion zone, very low conductivity (essentially open circuit until breakdown)

Shockley equation¶

$I_{D} = I_{S} (exp(V/V_{T}) - 1)$,

where $V_{T} = \frac{kT}{q} = \frac{RT}{F} = 26mV$ (Thermal voltage)

Forward bias: shrinking depletion zone
Reverse bias: widening depletion zone, very low conductivity (essentially open circuit until breakdown)

Three representations of diodes¶

Assuming there are internal resistance ($R_D$), threshold voltage ($V_D$).
* For $V \le V_D$, open circuit.
* For $V \geq V_D$, equivalent to a reverse voltage source of $V_D$.

Ideal diodes: $R_D = 0$, $V_D = 0$. Forward bias: short circuit. Reverse bias: open circuit.
With barrier voltage (Si = 0.6~0.7 V; Ge = 0.2~0.3V): $R_D = 0$, $V_D \neq 0$.
Practical diodes: $R_D \neq 0$, $V_D \neq 0$

Diode circuits¶

Transform diodes into equivalent components.

Source

Rectifiers¶

Only half wave rectification was covered.

Limiters (cutters)¶

Filters¶

When the load resistance is infinite (open circuit): peak detector

When the load resistance is finite:
The more discharging time scale ( $\tau = RC$ ), the less ripple voltage. ( $V_r \approx \frac{V_p}{fCR}$ when $V_r \ll V_p$ )

Voltage regulator using Zener diodes¶

Zener diode on Wikipedia

First unplug the Zener diode and solve the voltage across it.
Normally operates in reverse bias. ( $V_{Z}$ = 4-6 V )
When applied voltage > $V_{Z}$: Acts as a voltage source of $V_{Z}$. Open circuit otherwise.
When in forward bias: similar to regular diodes ( $V_{Z}$ = 0.7 V )
When breakdown $V_{Z}$ is independent of loading resistance.

BJT¶

Bipolar junction transistor on Wikipedia

Current control devices.

Symbol¶

NPN BJT (more common)

PNP BJT (less common nowadays)

B: Base
C: Collector
E: Emitter

Math¶

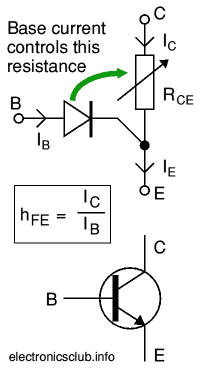
$I_C = \beta I_B$, $\beta \gg 1$ (typically 80-180)
$I_E = I_C + I_B = (1 + \beta) I_B$
BArrier voltage: $V_{BE} \approx 0.7$ Volt for Si BJT. 1.1 V for GaN BJT.
$I_{Csat} \approx \frac{V_{CC}-0.2}{R_C + R_E}$
$\beta I_B = I_C \leq I_{Csat}$

The rest is regular circuit analysis (KCL, KVL).

One could use the fact that $I_B$ is very small ($\mu A$) compared to other currents ($mA$).

MOSFET¶

MOSFET on wikipedia

Voltage control devices.

Gate voltage $V_{GS}$ is greater than threshold ($V_t$): low resistance, (ideally) short circuit.
Otherwise, high resistance, (ideally) open circuit.

Applied electricity

Course information¶

TL;DR¶

Current¶

Voltage¶

Dependent sources¶

Power balance¶

Resistive circuits, Nodal and mesh analysis¶

Nodal analysis¶

Loop (mesh) analysis¶

Series / parallel circuits¶

Resistor tolerance¶

Y-Δ transformation¶

Question¶

The principle of superposition¶

Thevenin and Norton equivalent circuits¶

For dependent sources¶

Maximum power transfer¶

Norton's theorem¶

Capacitors and Capacitance¶

Inductors and Inductance¶

AC steady-state analysis¶

RMS (Root mean square), effective value¶

Phase lead / lag¶

Complex algebra¶

Impedance¶

Filter¶

RC, RL, and RLC circuits¶

RC transients¶

RL transient¶

RLC transients¶

Damping¶

Quality factor¶

Steady state power analysis¶

Maximum power transfer¶

Power factor and complex power¶

Active power vs reactive power¶

Safety considerations¶

Magnetically coupled circuits¶

Mutual inductance¶

Energy analysis¶

Transformers¶

Frequency response¶

Series RLC¶

Bode plot¶

Multistage system¶

Network transfer function¶

Bandwidth¶

Quality factor and effective bandwidth¶

Poles and Zeros¶

Filters¶

OP-Amp¶

Ideal OP-Amp¶

Circuit analysis in Ideal OP-Amp¶

More OP-Amp circuits¶

Multiple input voltages¶

With energy-storing devices¶

Semiconductors¶

Materials¶

Why semi-conductivity¶

Carriers¶

P-N junctions and diodes¶

Depletion zone¶

Applying voltage¶

Shockley equation¶

Three representations of diodes¶

Diode circuits¶

Rectifiers¶

Limiters (cutters)¶

Filters¶

Voltage regulator using Zener diodes¶

BJT¶

Symbol¶

Math¶

MOSFET¶

Comments