Plots.jl gallery

Sources:

• goropikari/PlotsGallery.jl (repo archived)

• Julia Plots docs

Attributes

https://docs.juliaplots.org/stable/attributes/

using Plots
using Random
Random.seed!(2024)

Random.TaskLocalRNG()

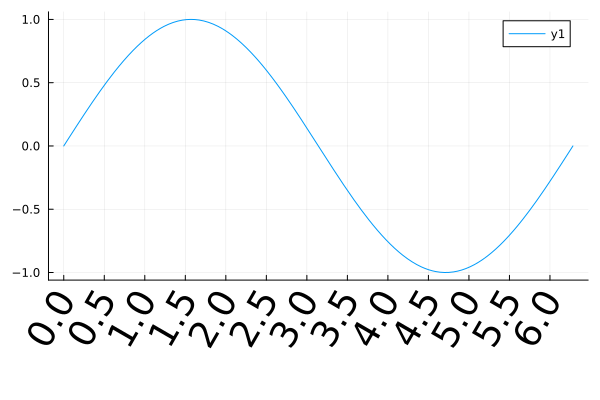
Ticks size and properties

plot(sin, 0, 2π;
    xticks=0:0.5:2π,
    xrotation=60,
    xtickfontsize=25,
    bottom_margin=15Plots.mm)

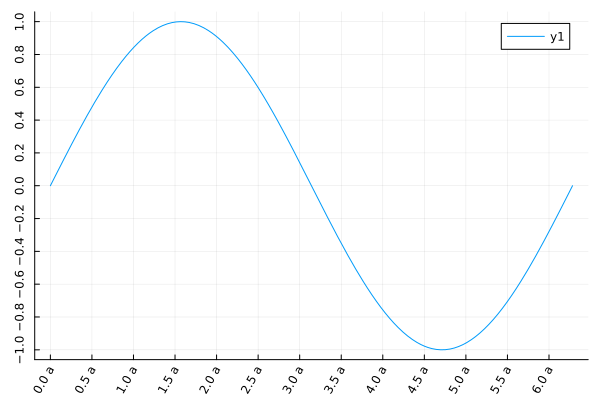
plot(sin, 0, 2π;
    xtick=(0:0.5:2π, ["$i a" for i in 0:0.5:2π]),
    ytick=-1:0.2:1,
    xrotation=60,
    yrotation=90,
)

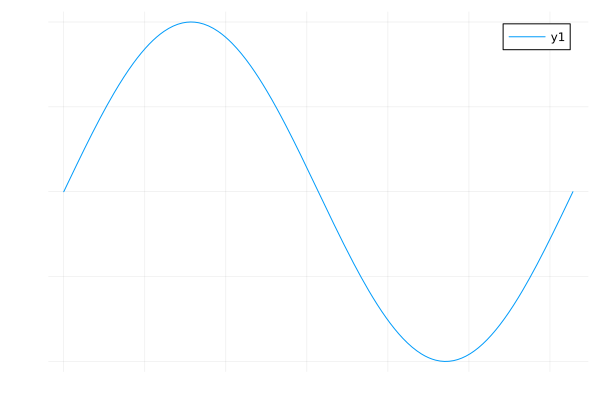
No axis

axis=false

plot(sin, 0, 2π, axis=false)

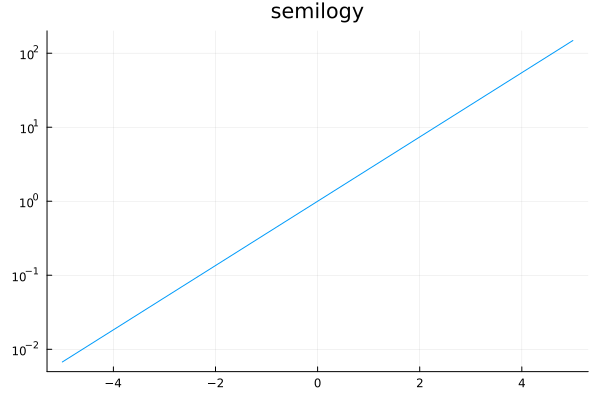
Log scale for axes

xscale=:log10, yscale=:log10

plot(exp, -5, 5, yscale=:log10, title="semilogy", legend=nothing)

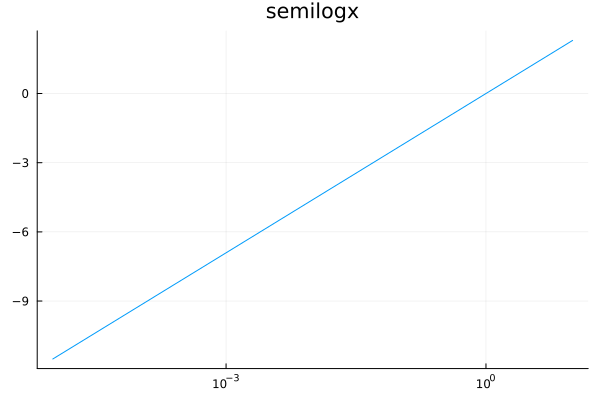
plot(log, 1e-5, 10, xscale=:log10, title="semilogx", legend=nothing)

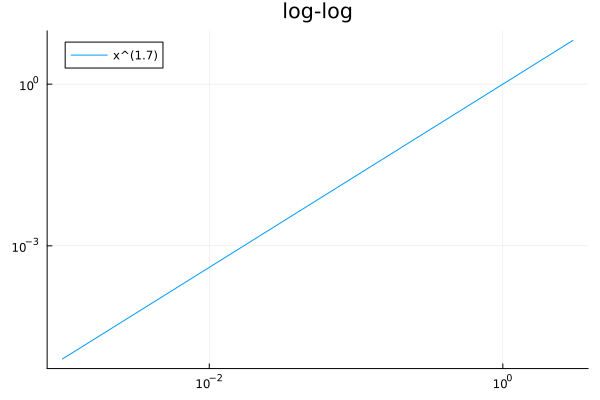
plot(x->x^1.7, 1e-3, 3, scale=:log10, title="log-log", label="x^(1.7)", legend=:topleft)

Axis range

xlims and ylims

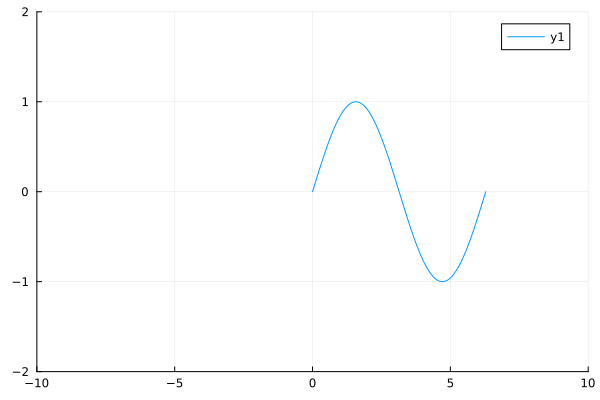
plot(sin, 0, 2π, xlims=(-10, 10), ylims=(-2,2))

Scientific notation

yformatter=:scientific

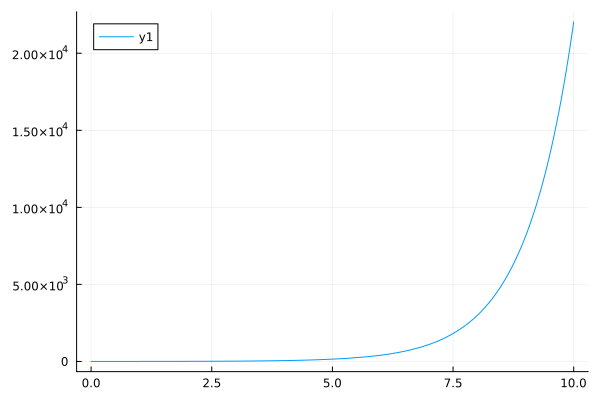
plot(exp, 0, 10, yformatter=:scientific)

Flip

xflip=true and/or yflip=true

plot(identity, 0:0.01:2π, proj=:polar, xflip=true, yflip=true, legend=false)

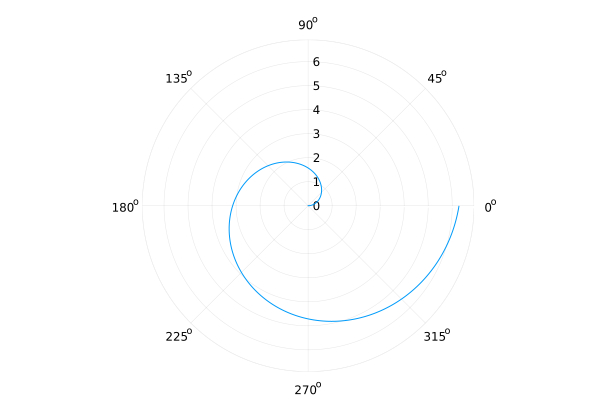
Aspect ratio

aspect_ratio=:equal or aspect_ratio=<number>

heatmap(bitrand(10, 10), aspect_ratio=:equal, c=:blues, colorbar=false)

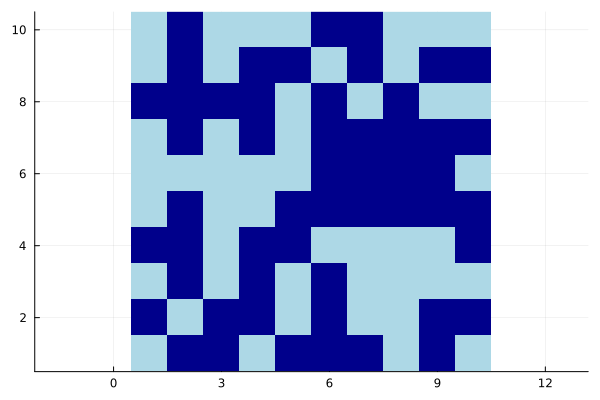
Fonts

LaTeX fonts are supported by the LaTeXStrings.jl package.

using Plots
using LaTeXStrings

plot(sin, 0, 2π,
    title=L"y = \sin(x)",
    titlefont=font(40), ## title

    xlabel=L"x",
    ylabel="y",
    xguidefontsize=30, ## x-guide
    yguidefontsize=20, ## y-guide
    # guidefontsize=20, ## both x,y-guide

    xtick=(0:0.5:2π, ["\$ $(i) \$" for i in 0:0.5:2π]),
    ytick=-1:0.5:1,
    xtickfontsize=15,
    ytickfontsize=20,
    # tickfontsize=10, ## for both x and y

    label="Sin function",
    legendfontsize=12,

    xlims=(0,2π),
    ylims=(-1,1),
    bottom_margin=5Plots.mm,
    left_margin=10Plots.mm,
    top_margin=15Plots.mm
)

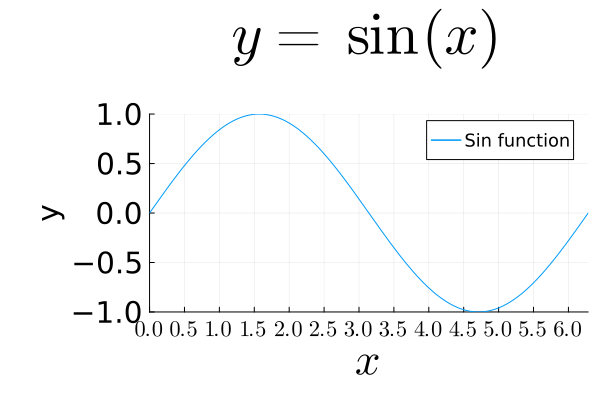
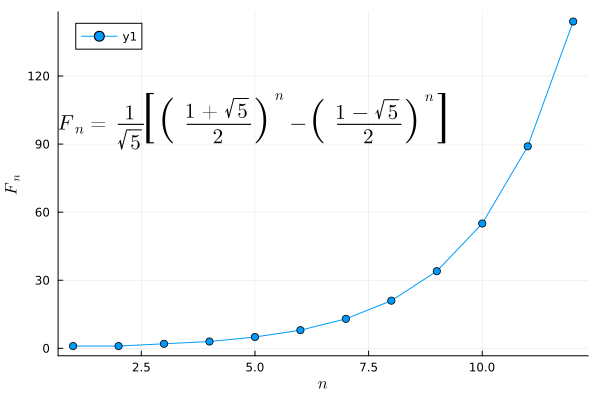
fib(x) = (((1+sqrt(5))/2)^x - ((1-sqrt(5))/2)^x)/sqrt(5)

ann = L"F_n = \frac{1}{\sqrt{5}} \left[\left( \frac{1+\sqrt{5}}{2} \right)^n - \left( \frac{1-\sqrt{5}}{2} \right)^n \right]"

plot(fib, 1:12, marker=:circle, xlabel=L"n", ylabel=L"F_n", annotation=(5, 100, ann))

Bar plots

using Plots
using StatsPlots
using StatsBase

measles = [38556, 24472, 14556, 18060, 19549, 8122, 28541, 7880, 3283, 4135, 7953, 1884]
mumps = [20178, 23536, 34561, 37395, 36072, 32237, 18597, 9408, 6005, 6268, 8963, 13882]
chickenPox = [37140, 32169, 37533, 39103, 33244, 23269, 16737, 5411, 3435, 6052, 12825, 23332]
ticklabel = string.(collect('A':'L'))

12-element Vector{String}:
 "A"
 "B"
 "C"
 "D"
 "E"
 "F"
 "G"
 "H"
 "I"
 "J"
 "K"
 "L"

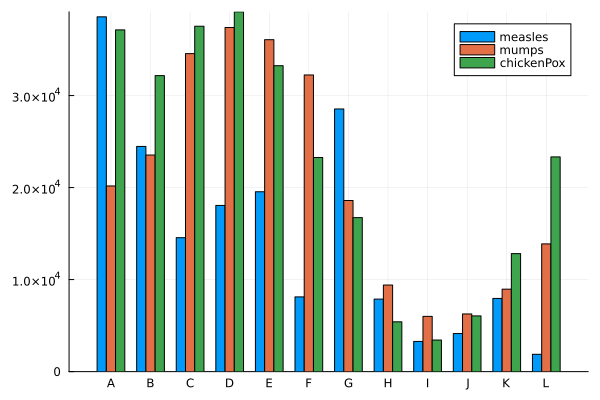
Grouped vertical bar plots

Requires the StatsPlots.jl package. groupedbar(data, bar_position = :dodge)

groupedbar([measles mumps chickenPox], bar_position = :dodge, bar_width=0.7, xticks=(1:12, ticklabel), label=["measles" "mumps" "chickenPox"])

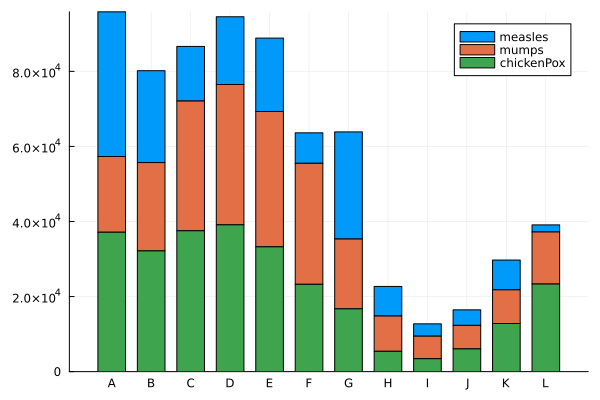
Stacked vertical bar plots

Requires StatsPlots package. groupedbar(data, bar_position = :stack)

groupedbar([measles mumps chickenPox],
        bar_position = :stack,
        bar_width=0.7,
        xticks=(1:12, ticklabel),
        label=["measles" "mumps" "chickenPox"])

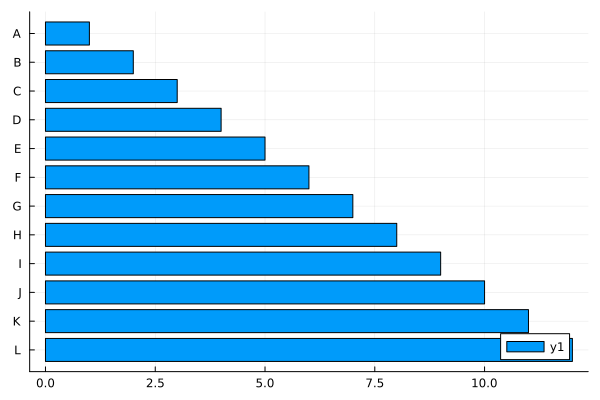
Horizontal Bar Plot

bar(data, orientation=:h)

bar(1:12, orientation=:h, yticks=(1:12, ticklabel), yflip=true)

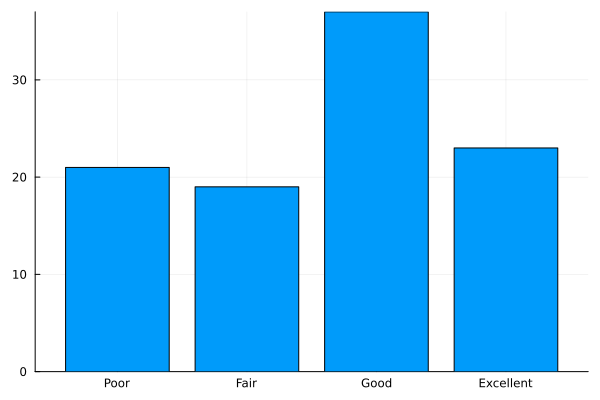
Categorical Histogram Plot

status = ["Poor", "Fair", "Good", "Excellent"]
data = sample(status, Weights([1,1,2,2]), 100)
datamap = countmap(data)

bar((x -> datamap[x]).(status), xticks=(1:4, status), legend=nothing)

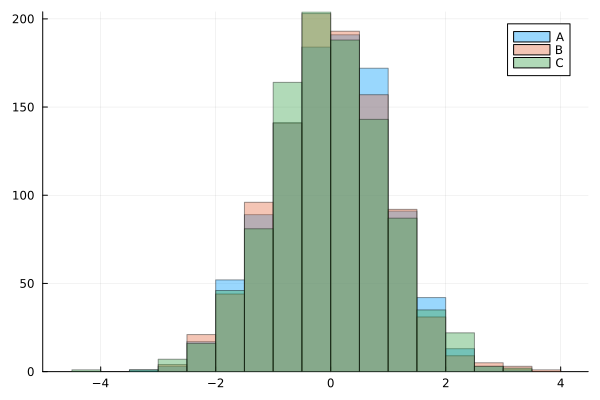
Histogram

histogram(data, bins=N)

using Plots

x = randn(1000)
y = randn(1000)
z = randn(1000)

histogram(x, bins=20, alpha=0.4, label="A")
histogram!(y, bins=20, alpha=0.4, label="B")
histogram!(z, bins=20, alpha=0.4, label="C")

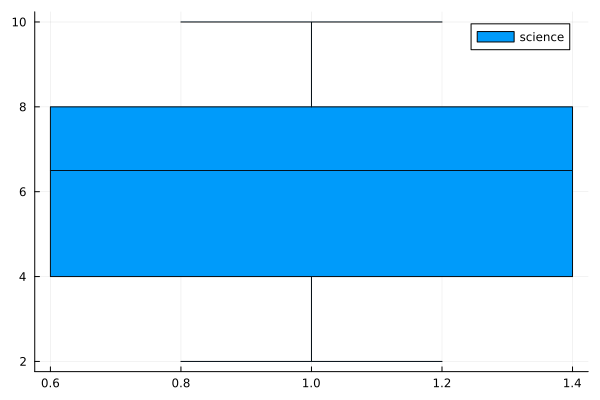
Box plots

using Plots
using StatsPlots
using Statistics

n = 30
science = rand(1:10, n)
boxplot(science, label="science")

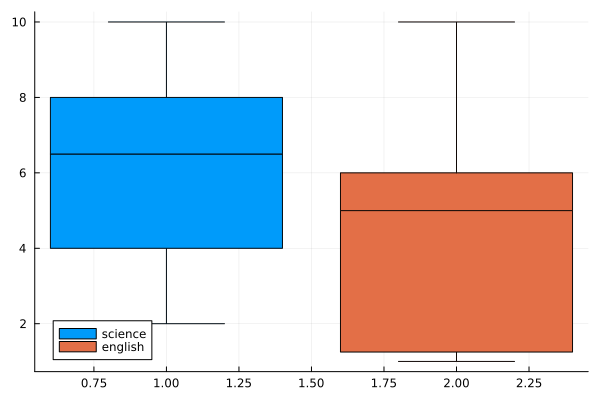
english = rand(1:10, n)
boxplot([science english], label=["science" "english"])

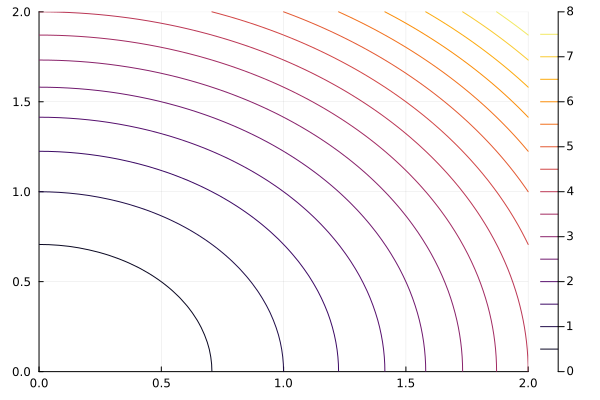
Contour Plots

Over a function

contour(xs, ys, f) where z = f(x, y)

using Plots

xs = range(0, stop=2, length=50)
ys = range(0, stop=2, length=50)
f = (x , y) -> x^2 + y^2

contour(xs, ys, f)

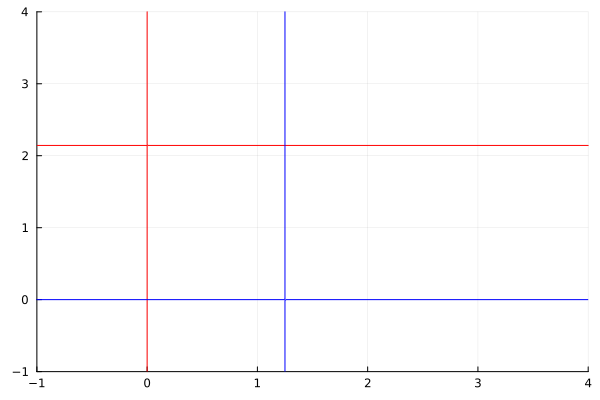
Nullclines

Nullclines (zero-growth isoclines) are curves where the derivative of one variable is zero. Nullclines are used to analyze evolution and stability of ODE systems.

using Plots

dx = (x, y) -> 3x - 1.4x*y
dy = (x, y) -> -y + 0.8x*y

myrange = -1:0.01:4

contour(myrange, myrange, dx, levels=[0], color=:red, legend=false)
contour!(myrange, myrange, dy, levels=[0], color=:blue, legend=false)

Contour plot over an array

contour(x1d, y1d, xy2d)

# Notice xs is transposed
# This makes zz a 2D matrix
zz = f.(xs', ys)
contour(xs, ys, zz)

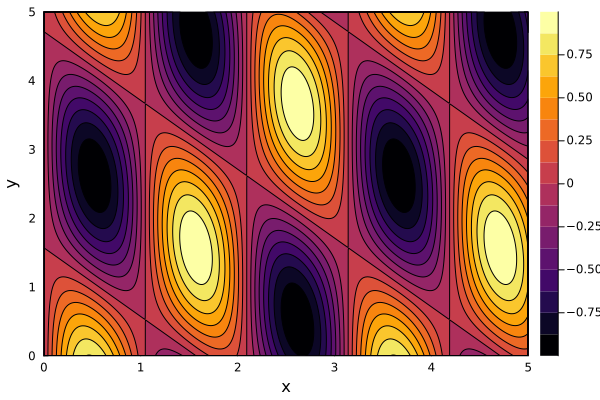
Filled Contour Plots

• contour(xs, ys, f, fill=true)

• contourf(xs, ys, f)

contour(0:0.01:5, 0:0.01:5, (x, y) -> sin(3x) * cos(x+y), xlabel="x", ylabel="y", fill=true)

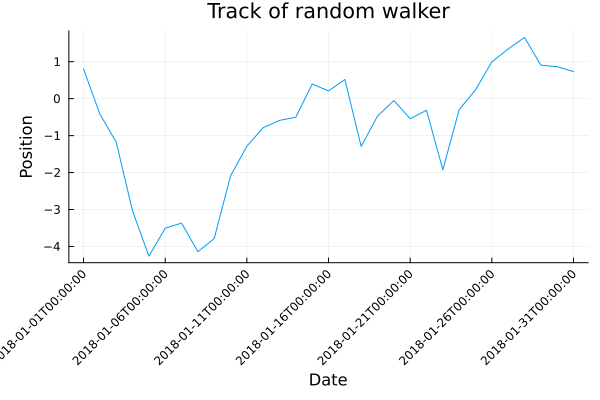
Datetime plot

• Use Dates package and Data data type

• Customize ticks

using Plots
using Dates

days = 31
position = cumsum(randn(days))
x = Date(2018,1,1):Day(1):Date(2018,1,31)
ticks = [x[i] for i in 1:5:length(x)]

plot(x, position,
     xlabel="Date",
     ylabel="Position",
     title="Track of random walker",
	 legend=nothing,
     xticks=ticks,
     xrotation=45,
     bottom_margin=10Plots.mm,
     left_margin=5Plots.mm)

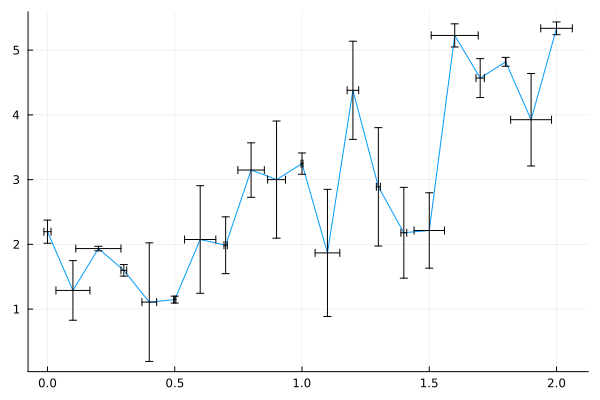
Error bar

plots(..., xerr=xerr, yerr=yerr)

using Plots

f = x -> 2 * x + 1
x = 0:0.1:2
n = length(x)
y = f.(x) + randn(n)

plot(x, y,
    xerr=0.1 * rand(n),
    yerr=rand(n),
	legend=nothing)

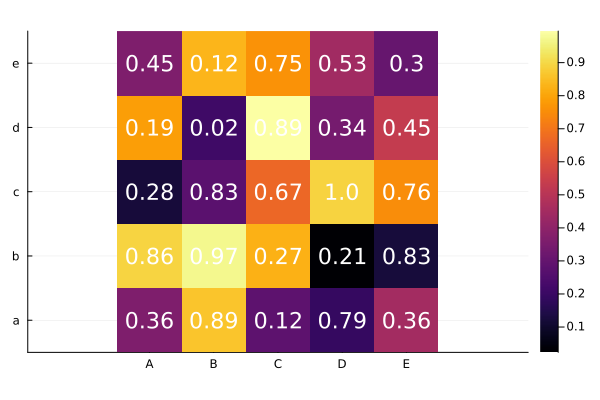
Heatmap

heatmap(data)

using Plots

a = rand(5,5)
xlabel = string.(collect('A':'E'))
ylabel = string.(collect('a':'e'))
heatmap(a, xticks=(1:5, xlabel),
           yticks=(1:5, ylabel),
           aspect_ratio=:equal)

fontsize = 15
nrow, ncol = size(a)

# Add number annotations to plots
ann = [(i,j, text(round(a[i,j], digits=2), fontsize, :white, :center))
            for i in 1:nrow for j in 1:ncol]

annotate!(ann, linecolor=:white)

Line plots

using Plots
plot(x, y)
plot(f, xRange)
plot(f, xMin, xMax)
plot(x, [y1 y2])

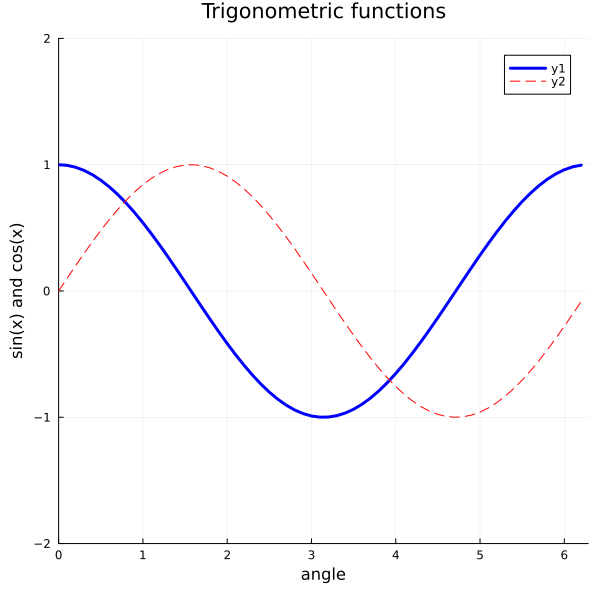
using Plots

# Data
x = 0:0.1:2pi
y1 = cos.(x)
y2 = sin.(x)

# Creating a plot in steps
plot(x, y1, color="blue", linewidth=3)
plot!(x, y2, color="red", line=:dash)
title!("Trigonometric functions")
xlabel!("angle")
ylabel!("sin(x) and cos(x)")
plot!(xlims=(0,2pi), ylims=(-2, 2), size=(600, 600))

plot(x, y1, line=(:blue, 3))
plot!(x, y2, line=(:dash, :red))

# Use keywords to set the options all in one plot() call
plot!(title="Trigonometric functions",
        xlabel="angle",
        ylabel="sin(x) and cos(x)",
        xlims=(0,2pi), ylims=(-2, 2), size=(600, 600))

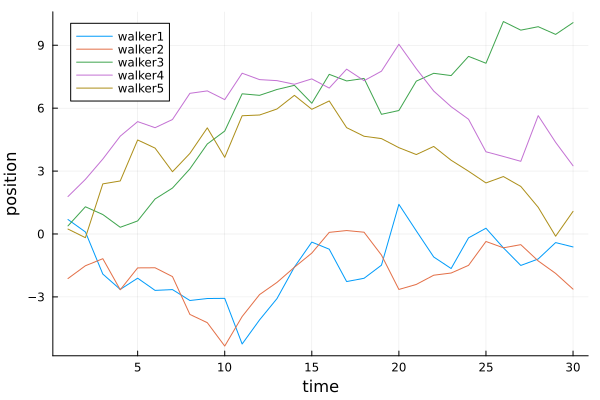
Plotting multiple series

• One row = one observation

• One column = one species

time = 30
walker1 = cumsum(randn(time))
walker2 = cumsum(randn(time))
walker3 = cumsum(randn(time))
walker4 = cumsum(randn(time))
walker5 = cumsum(randn(time))
plot(1:time, [walker1 walker2 walker3 walker4 walker5],
    xlabel="time", ylabel="position",
    label=["walker1" "walker2" "walker3" "walker4" "walker5"],
    legend=:topleft
)

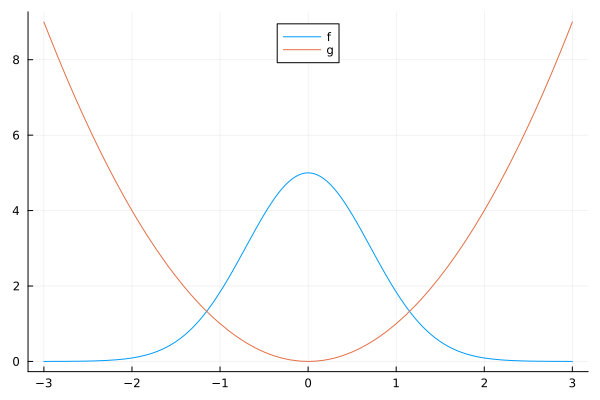
Parametric plots

Functions can be plotted directly.

• plot(f, xmin, xmax)

• plot(f, range_of_x)

• plot(fx(t), fy(t), range_of_t)

let
    f = x -> 5exp(-x^2)
    g = x -> x^2
    plot([f, g], -3, 3, label=["f" "g"], legend=:top)
end

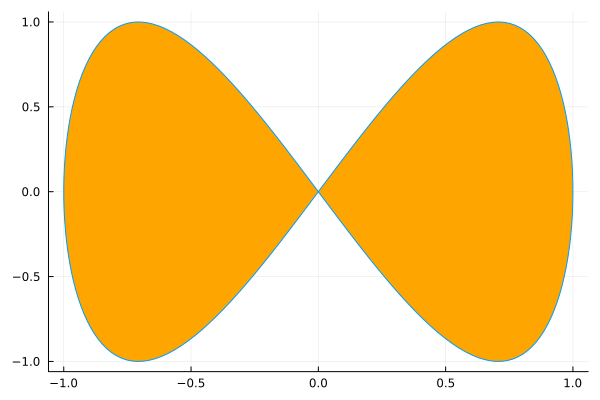
plot(sin, t->sin(2t), 0, 2π, leg=false, fill=(0,:orange))

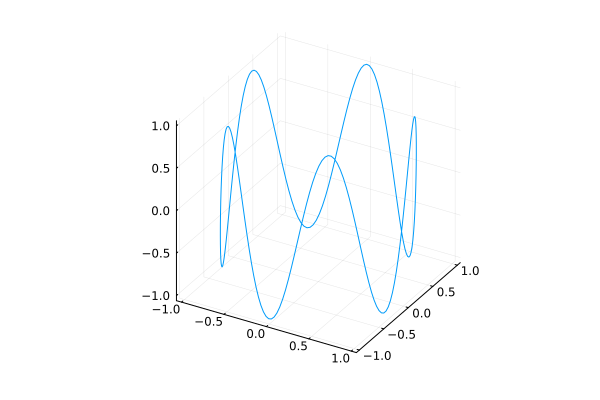
3D line plot

Similar to 2D line plots.

plot(fx(t), fy(t), fz(t), tmin, tmax [, kwargs...])

plot(cos, sin, t -> sin(5t), 0, 2pi, legend=nothing)

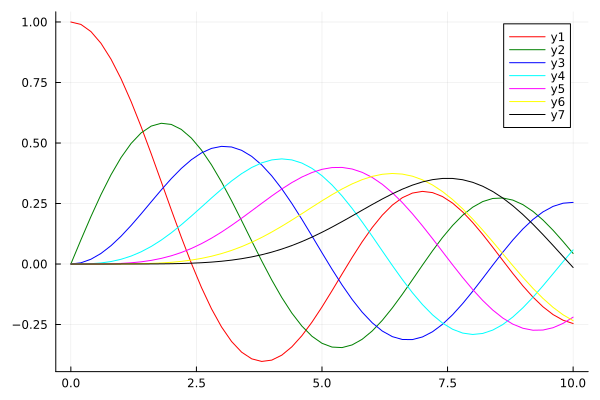
Line colors

plot(x, y, c=color)

using Plots
using SpecialFunctions

x = 0:0.2:10
y0 = besselj.(0,x)
y1 = besselj.(1,x)
y2 = besselj.(2,x)
y3 = besselj.(3,x)
y4 = besselj.(4,x)
y5 = besselj.(5,x)
y6 = besselj.(6,x)
colors = [:red :green :blue :cyan :magenta :yellow :black]
plot(x, [y0 y1 y2 y3 y4 y5 y6], c=colors)

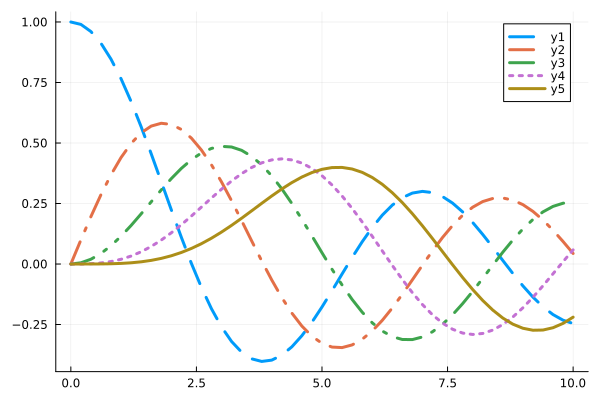
Line styles

using Plots
@show Plots.supported_styles()

Plots.supported_styles() = [:auto, :dash, :dashdot, :dashdotdot, :dot, :solid]

6-element Vector{Symbol}:
 :auto
 :dash
 :dashdot
 :dashdotdot
 :dot
 :solid

style = Plots.supported_styles()[2:end]
style = reshape(style, 1, length(style))
plot(x, [y0 y1 y2 y3 y4], line=(3, style))

Polar Plots

plot(θ, r, proj=:polar)

using Plots
plot(θ -> 1 + cos(θ) * sin(θ)^2, 0, 2π, proj=:polar, lims=(0, 1.5))

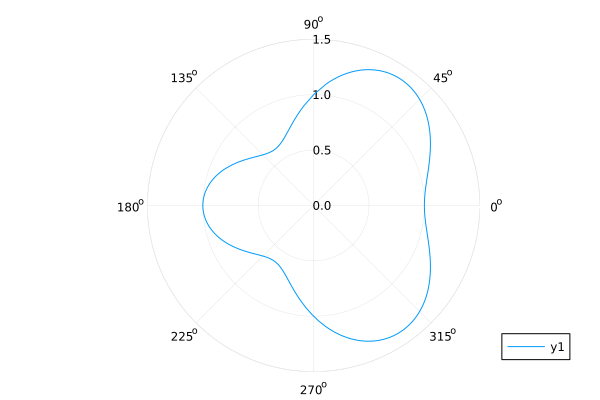
Rose Plots

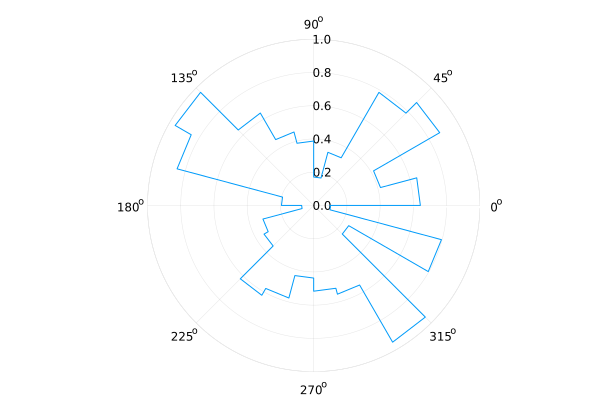
plot(..., proj=:polar, line=:steppre)

n = 24
R = rand(n+1)
plot(0:2pi/n:2pi, R, proj=:polar, line=:steppre, lims=(0, 1), legend=nothing)

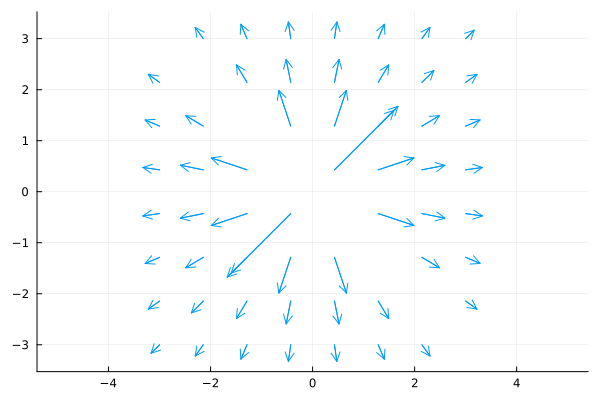
Quiver Plots

• quiver(x1d, y1d, quiver=(vx1d, vy1d)

• quiver(x2d, y2d, quiver=(x, y)->(u, v))

using Plots

n = 7
f = (x,y) -> hypot(x, y) |> inv

x = repeat(-3:(2*3)/n:3, 1, n) |> vec
y = repeat(-3:(2*3)/n:3, 1, n)' |> vec
vx = f.(x,y) .* cos.(atan.(y,x)) |> vec
vy = f.(x,y) .* sin.(atan.(y,x)) |> vec
quiver(x, y, quiver=(vx, vy), aspect_ratio=:equal)

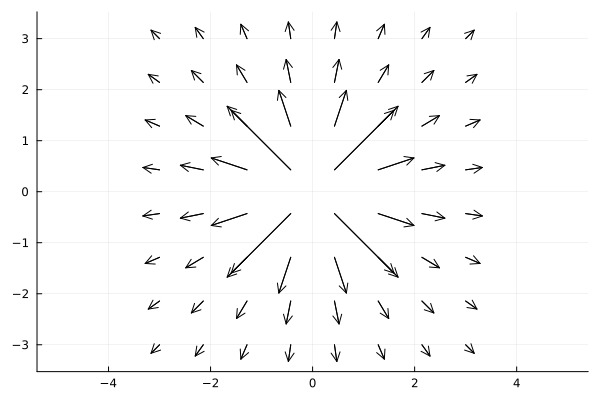
g = (x, y) -> [f(x,y) * cos(atan(y,x)), f(x,y) * sin(atan(y,x))]
xx = [x for y in -3:(2*3)/n:3, x in -3:(2*3)/n:3]
yy = [y for y in -3:(2*3)/n:3, x in -3:(2*3)/n:3]
quiver(xx, yy, quiver=g, aspect_ratio=:equal, color=:black)

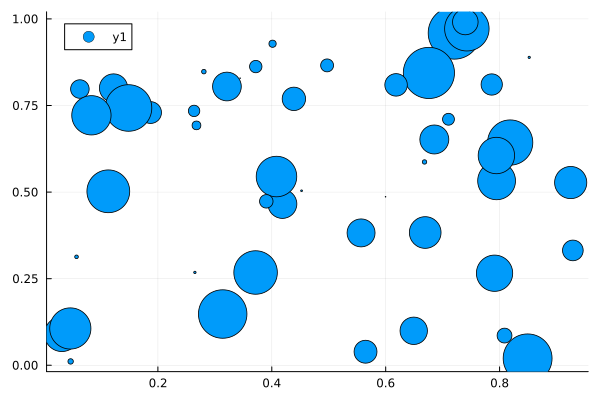
Scatter Plots

2D Scatter Plots: scatter(xpos, ypos)

using Plots

n = 50
x = rand(n)
y = rand(n)
ms = rand(50) * 30
scatter(x, y, markersize=ms)

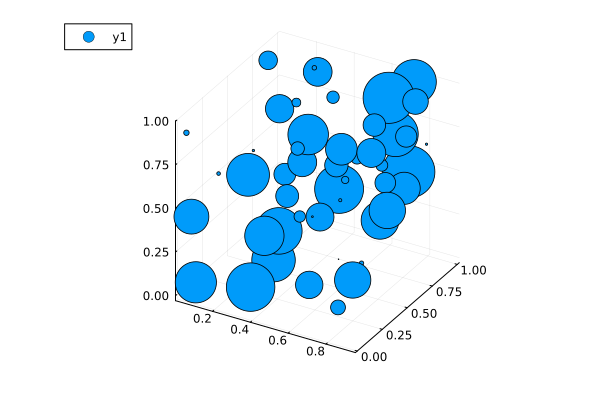
3D Scatter Plots: scatter(xpos, ypos, zpos)

scatter(x, y, rand(n), markersize=ms)

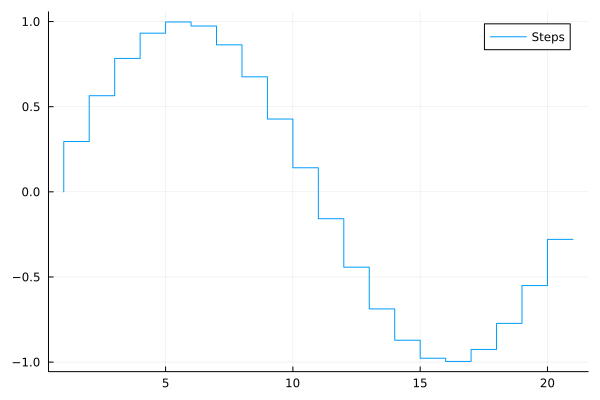
Stairstep plot

plot(..., line=:steppre)

plot(sin.(0:0.3:2pi), line=:steppre, label="Steps")

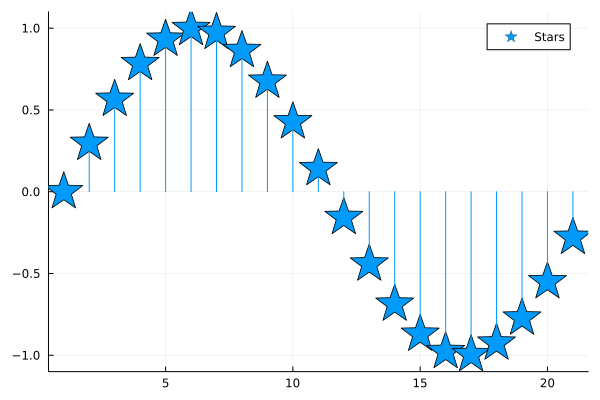
Stem plot

Known as the lollipop plot.

plot(..., line=:stem)

plot(sin.(0:0.3:2pi), line=:stem, marker=:star, markersize=20, ylims=(-1.1, 1.1), label="Stars")

Subplots

• plot(p1, p2, p3, ...)

• plot(..., layout=(nrow, ncol))

• plot(..., layout=@layout [...])

Source

using Plots

data = rand(100, 4)

100×4 Matrix{Float64}:
 0.709981   0.973362  0.516176   0.363075
 0.761391   0.388399  0.193247   0.724163
 0.75949    0.815402  0.0369112  0.137228
 0.761702   0.902961  0.330324   0.455833
 0.795277   0.416984  0.945352   0.176323
 0.586307   0.286339  0.499248   0.0763004
 0.276137   0.765012  0.594053   0.294608
 0.84172    0.687983  0.841599   0.620266
 0.847136   0.393362  0.305451   0.216803
 0.380462   0.687962  0.794865   0.127923
 ⋮                               
 0.378577   0.106089  0.691953   0.777491
 0.0571538  0.977407  0.276459   0.607869
 0.674539   0.610381  0.236658   0.662346
 0.278811   0.179141  0.604079   0.515615
 0.695049   0.514618  0.438862   0.922791
 0.924816   0.210846  0.912419   0.860384
 0.508744   0.798775  0.132198   0.429291
 0.5701     0.786537  0.709826   0.66473
 0.83062    0.233978  0.425281   0.375258

create a 2x2 grid, and map each of the 4 series to one of the subplots

plot(data, layout = 4)

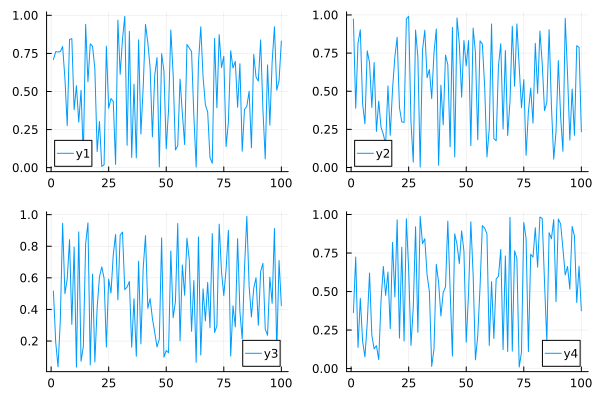
More complex grid layouts can be created with the grid(…) constructor:

plot(data, layout = grid(4, 1, heights=[0.1 ,0.4, 0.4, 0.1]))

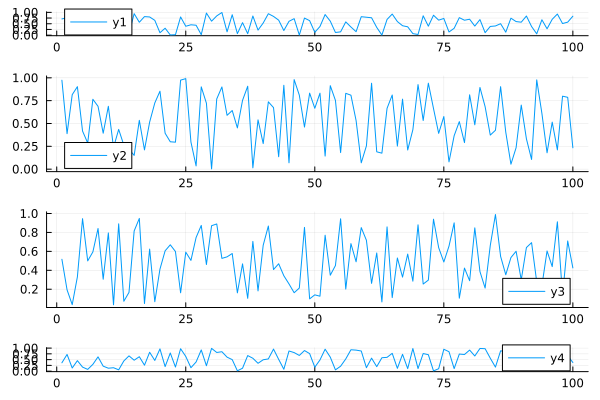
Adding titles and labels

plot(data, layout = 4, label=["a" "b" "c" "d"], title=["1" "2" "3" "4"])

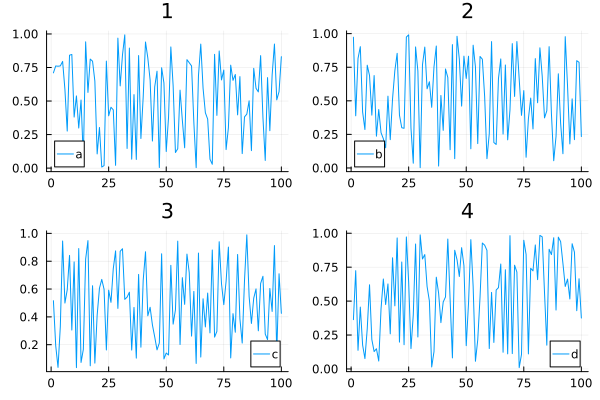
Use @layout macro

l = @layout [
    a{0.3w} [grid(3,3)
             b{0.2h}  ]
]
plot(
    rand(10, 11),
    layout = l, legend = false, seriestype = [:bar :scatter :path],
    title = ["($i)" for j in 1:1, i in 1:11], titleloc = :right, titlefont = font(8)
)

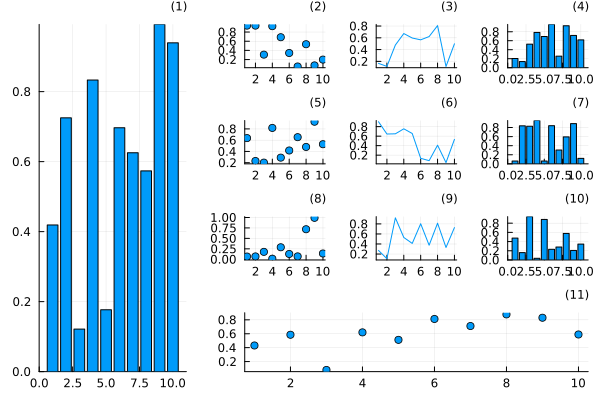
Use _ to ignore a spot in the layout

plot((plot() for i in 1:7)..., layout=@layout([_ ° _; ° ° °; ° ° °]))

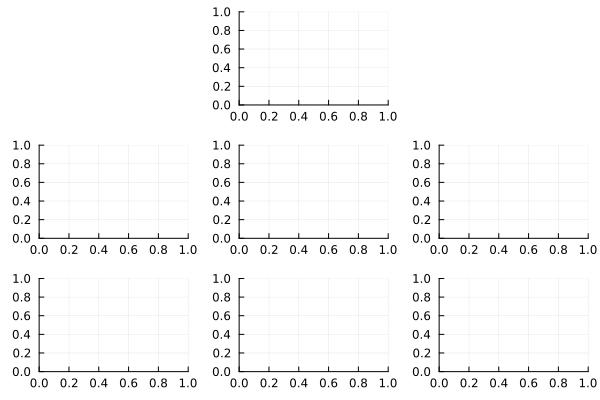
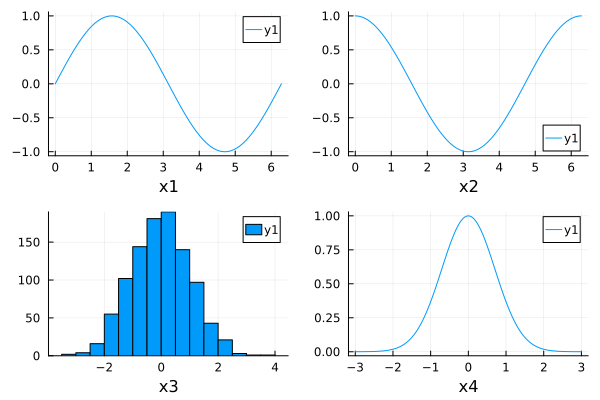
Build subplots one by one

p1 = plot(sin, 0, 2pi, xlabel="x1")
p2 = plot(cos, 0, 2pi, xlabel="x2")
p3 = histogram(randn(1000), xlabel="x3")
p4 = plot(x->exp(-x^2), -3, 3, xlabel="x4")
plot(p1, p2, p3, p4)

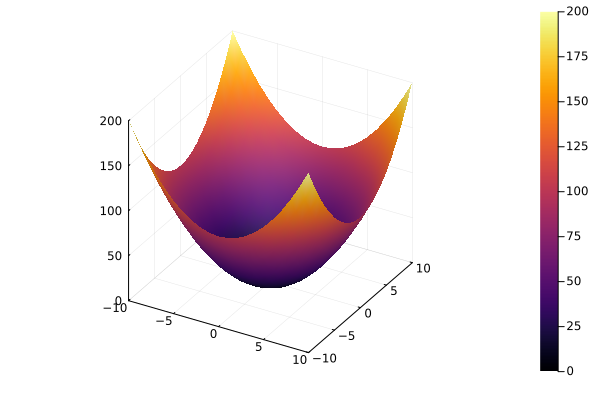
Surface plots

• surface(x, y, z)

• surface(x, y, (x,y)->z)

• plot(x, y, z, linetype=:surface)

• plot(x, y, z, linetype=:wireframe)

using Plots

x = y = -10:10
f = (x , y) -> x^2 + y^2

surface(x, y, f)

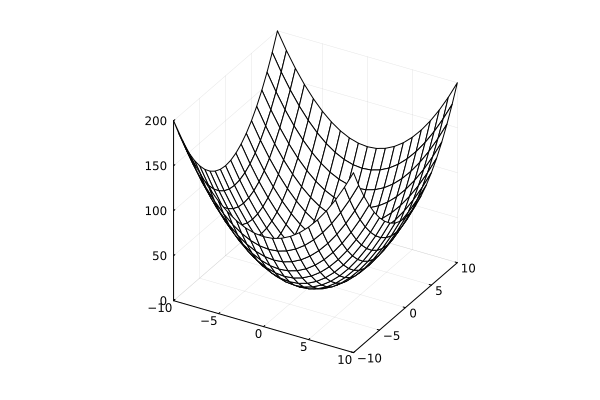
surface style

plot(x, y, f, linetype=:surface)

wireframe style

plot(x, y, f, linetype=:wireframe)

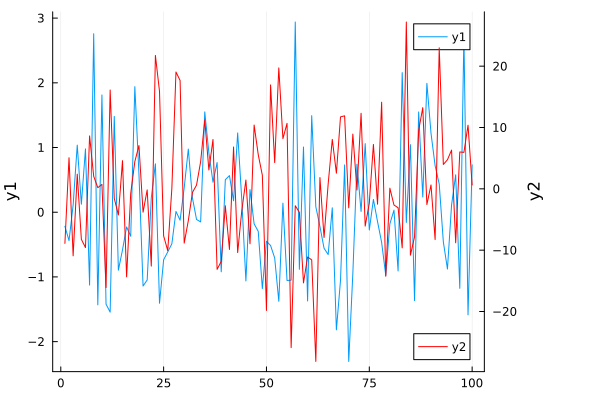
Twin Y Axis

plot!(twinx())

using Plots

plot(randn(100), ylabel="y1", leg=:topright)
plot!(
    twinx(), randn(100)*10,
    c=:red,
    ylabel="y2",
    leg=:bottomright,
    size=(600, 400)
)
plot!(right_margin=15Plots.mm)

Animations

using Plots

define the Lorenz attractor

Base.@kwdef mutable struct Lorenz
    dt::Float64 = 0.02
    σ::Float64 = 10
    ρ::Float64 = 28
    β::Float64 = 8/3
    x::Float64 = 1
    y::Float64 = 1
    z::Float64 = 1
end

function step!(l::Lorenz)
    dx = l.σ * (l.y - l.x)
    dy = l.x * (l.ρ - l.z) - l.y
    dz = l.x * l.y - l.β * l.z
    l.x += l.dt * dx
    l.y += l.dt * dy
    l.z += l.dt * dz
end

attractor = Lorenz()

Main.var"##230".Lorenz(0.02, 10.0, 28.0, 2.6666666666666665, 1.0, 1.0, 1.0)

initialize a 3D plot with 1 empty series

plt = plot3d(
    1,
    xlim = (-30, 30),
    ylim = (-30, 30),
    zlim = (0, 60),
    title = "Lorenz Attractor",
    marker = 2,
)

plt

pushing new points to the plot

anim = @animate for i=1:1500
    step!(attractor)
    push!(plt, attractor.x, attractor.y, attractor.z)
end

mp4(anim, fps = 15)

[ Info: Saved animation to /tmp/jl_j8Dkxyx8BO.mp4

---

This notebook was generated using Literate.jl.